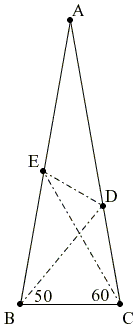
Let ABC be an isosceles triangle (AB = AC) with BAC = 20°. Point D is on side AC such that CBD = 50°. Point E is on side AB such that BCE = 60°. Find the measure of CED.

Solution

Copyright © 1996-2008 Alexander Bogomolny

This is Solution 8 from [Knop] and is due to Sergey Saprikin, a high school student at the time.

Let T be the intersection of the bisector of angle ACB with the side AB.

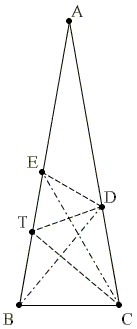
Then BTC = 60°, and, since BC = CD, ΔBCT = ΔDCT. Hence CTD = 60°.

In ΔCDT, E is the intersection of the angle bisector at C and of the external angle bisector T. T is then one of the excenters of ΔCDT. It follows that, in that triangle, DE is the external bisector of the angle at D. BDT = DBT = 30°. Next, CDT = 80°, EDT = (180° - 80°)/2 = 50°, and, finally, CED = 180° - 20° - 50° - 30° - 50° = 30°.

Reference

1. C. Knop, Nine Solutions to One Problem, Kvant, 1993, no 6.

Copyright © 1996-2008 Alexander Bogomolny