The 80-80-20 Triangle Problem, Solution #10
| |
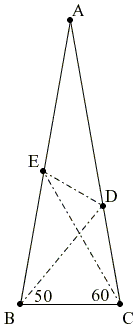
Let ABC be an isosceles triangle (AB = AC) with  BAC = 20°. Point D is on side AC such that CBD = 50°. Point E is on side AB such that BCE = 60°. Find the measure of CED.
|
Solution
Copyright © 1996-2008 Alexander Bogomolny
The proof is due to Luke Rapley.
With radius CE and center C sweep an arc to intersect BC at U and AC at V.
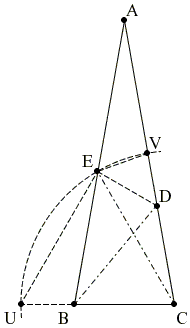
ΔCEU is isosceles (CE = CU) and, BCE being 60°, is also equilateral. In particular, EU = CE and CEU = 60°. It follows that BEU = 20°. Another preliminary result, viz., AE = CE, follows from the observation that ΔACE having angles at A and C both equal to 20° is isosceles.
We are going to compare triangles BEU and VAE:
AE = EU, since both equal CE,
AV = BE, because AV = AC - CV = AB - AE = BE,
EAV = BEU since both equal 20°.
We conclude that, by SAS, the two triangles are equal. From here we get EV = BU.
On the other hand, since ΔBCD is isosceles, BC = CD and consequently,
| |
BU = CU - BC = CV - CD = DV.
|
Therefore, VD = EV and triangle DEV is isosceles. Now,
| |
DVE = 180° - AVE = 180° - EBU = ABC = 80°.
|
So DEV = (180° - 80°)/2 = 50°. Counting angles around E, we see that CED = 30°.
Copyright © 1996-2008 Alexander Bogomolny
|
