The 80-80-20 Triangle Problem, Solution #1

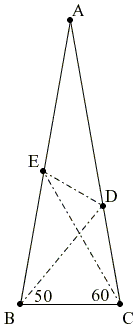
Let ABC be an isosceles triangle (AB = AC) with ∠BAC = 20°. Point D is on side AC such that ∠CBD = 50°. Point E is on side AB such that ∠BCE = 60°. Find the measure of ∠CED.

Solution

Draw ED'||BC, D' on AC. Let BD' meet CE in P. Since ΔBCP is equilateral, CP = BC. Since ΔBCD is isosceles, BC = CD. Hence ΔCDP is isosceles,

∠CPD = 80°,
∠DPD' = 40°.

Since ∠DD'P = 40°, ΔDPD' is isosceles and DP = DD'. Also, since ΔEPD' is equilateral, EP = ED'. Hence, by SSS, ΔDED' = ΔDEP, DE bisects ∠D'EP so that ∠CED = ∠PED = 30°.

Reference

H. S. M. Coxeter, S. L. Greitzer, Geometry Revisited, MAA, 1967, p. 159
C. Knop, Nine Solutions to One Problem, Kvant, 1993, no 6, Solution 1.

The 80-80-20 Triangle Problem

Solution #1
Solution #2
Solution #3
Solution #4
Solution #5
Solution #6
Solution #7
Solution #8
Solution #9
Solution #10
Solution #11
Solution #12

71543992