Eyeball Theorem Rectified
Problem
Points $C,E$ on $AB,$ with $AC$ and $BE$ being the diagonals of two similar rhombi, $AMCD$ and $BFEG.$ $H=AF\cap CD,$ $I=AG\cap CM,$ $J=BM\cap EG,$ $K=BD\cap EF,$ as shown.
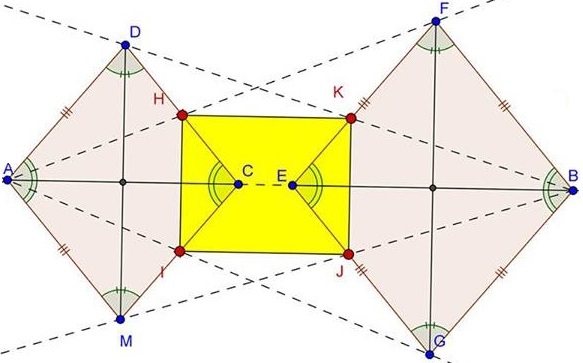
Prove that $HIJK$ is a rectangle.
Solution
Assume that in Cartesian plane the points have the following coordinates: $A=(-a,0),$ $C=(a,0),$ $D=(0,1),$ $M=(0,-1),$ $E=(b-am,0),$ $B=(b+am,0),$ $F=(b,m),$ $G=(b,-m),$ with $a,b,m \gt 0$ and $b-am\gt a.$ The straight lines involved have the equations:
$\begin{align}\displaystyle AF:\space&\frac{x+a}{a+b}=\frac{y}{m},\\ CD:\space&\frac{x}{a}+y=1,\\ AG:\space&\frac{x+a}{a+b}=-\frac{y}{m},\\ CM:\space&\frac{x}{a}-y=1. \end{align}$
If, for a generic point $S,$ $S=(x_{S},y_{S}),$ then, say, $x_{H}$ is the solution of $\displaystyle m\frac{x+a}{a+b}=1-\frac{x}{a},$ and so is $x_{I},$ showing $x_{H}=x_{I}.$ As straightforward is to show that $x_{K}=x_{J},$ $y_{H}=y_{K},$ and $y_{I}=y_{J}.$
Acknowledgment
The problem has been posted by Dao Thanh Oai (Vietnam) at the CutTheKnotMath facebook page. The solution is by Leo Giugiuc (Romania).
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
71547662
