Paper Folding And Cutting Sangaku

The following three problems are from the 1743 book Kanyjia Otogi Zoshi by Nakane Genjun (1701-1761) [Fukagawa and Rothman, pp. 76-77, pp. 85-87]. In an English translation, Collection of Interesting Results in Mathematics, it sounds almost like one of D. Wells' books (The Penguin Dictionary of Curious and Interesting Geometry, The Penguin Dictionary of Curious and Interesting Numbers and The Penguin Dictionary of Curious and Interesting Puzzles). And indeed it gives us samples of the Japanese recreational mathematics of the 18^th century. (Fukagawa and Rothman's book is devoted to a peculiar mathematical art of sangaku but they also took pains to highlight the historical background of Japan during the Edo period and along the way outline the biographies and work of many contemporary mathematicians, Nakane Genjun in particular.

Solutions

References

1. H. Fukagawa, A. Rothman, Sacred Mathematics: Japanese Temple Geometry, Princeton University Press, 2008

Copyright © 1996-2008 Alexander Bogomolny

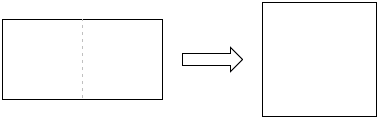
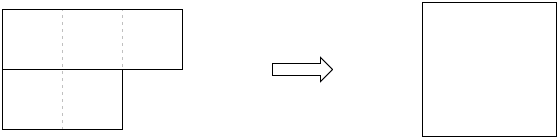
The first problem comes with two solutions which the diagram below make quite obvious.

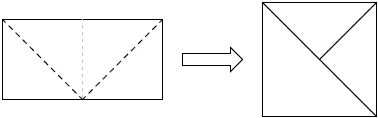
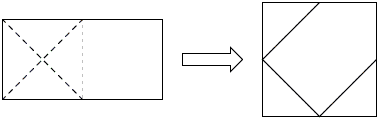
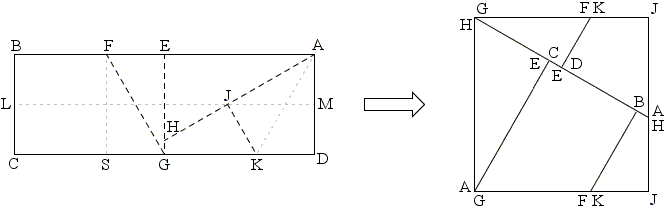
A solution to the second problem which is the least trivial of the three is presented by the following diagram where the light dotted lines indicate folds and the dashed lines indicate the cuts.

The diagram begs for an explanation. First fold the rectangle along the long axis LM. Then fold the corner D into J on LM. This will generate point K and divide angle at A into three equal angles of 30°. Indeed, in the right ΔAJM, AJ (= AD) is twice as long as the leg AM. Which makes angle AJM 30° and angle JAM 60°. And, since AK bisects angle JAM, all three angles at A are indeed equal. Observe that from the Pythagorean theorem JM = √3/2. Let H be the intersection of the fold along AJ and the short midline EG. From the similarity of triangles AJM and AHE, AH = JM = √3. Fold K to G and mark the new position of D as S. Fold vertically at S to get F. Triangles ADK and EGF are congruent so that angle EGF is also 30°. There are no other angles but 30°, 60°, and 120°.

Let's check the lengths. From ΔAKD, DK = √3/3 = JK. FG = 2EF = 2DK = 2√3/3 so that FG + JK = √3. And we see that the pieces do fit into a square.

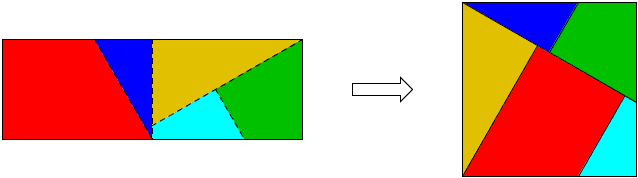
Here is the same decomposition with colored pieces.

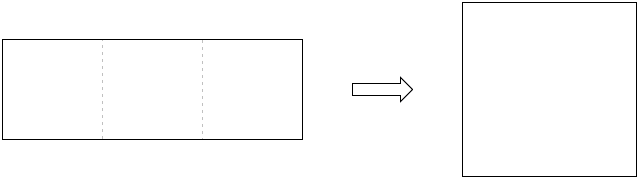
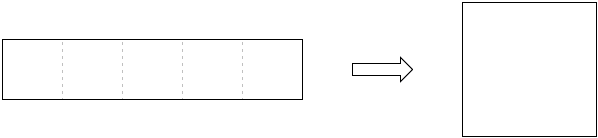
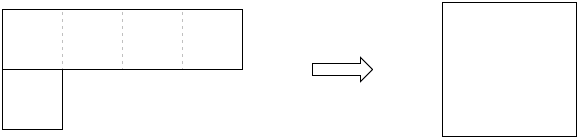
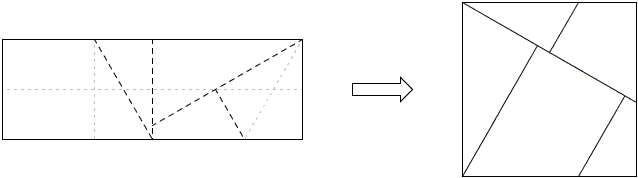
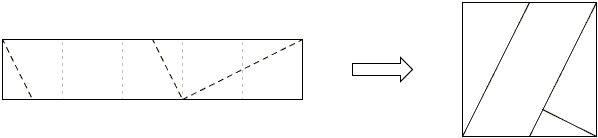
Solutions to the problems with five squares are shown by the diagrams and require little explanation if at all:

(a)

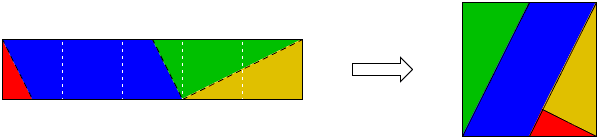
(b)

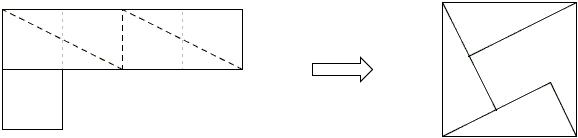
(c)

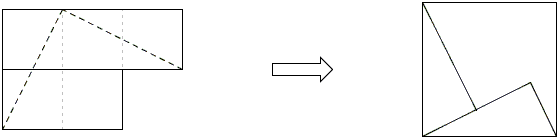
The latter is nothing but a proof of the Pythagorean theorem.

Paper Folding Geometry

• Angle Trisection by Paper Folding
• Angles in Triangle Add to 180^o
• Broken Chord Theorem by Paper Folding
• Dividing a Segment into Equal Parts by Paper Folding
• Egyptian Triangle By Paper Folding
• My Logo
• Paper Folding And Cutting Sangaku
• Parabola by Paper Folding
• Radius of a Circle by Paper Folding

Copyright © 1996-2008 Alexander Bogomolny