A Property of Semicircles:
What is this about?
A Mathematical Droodle

26 April 2015, Created with GeoGebra

The applet is intended to suggest a curious result published recently by Andrew K. Jobbings (The Mathematical Gazette, v. 95, n 534, Nov 2011, 538-540):

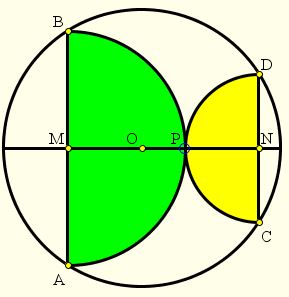
Assume AB and CD are parallel chords in a circle (O), with center O. Let M and N be the points of intersection of the diameter perpendicular to the chords with the chords. Assume, in addition, that the semicircles formed on the chords as diameters touch each other in point P on MN. Then the sum of the areas of the two semicircles is half the area of (O).

A property of touching semicircles - problem

The construction brings to mind the famous arbelos in which Archimedes himself showed keen interest. May it have as many properties as arbelos.

Let AB = 2a and CD = 2b, a and b being the radii of the two semicircles. Since the semicircles touch in P, MN = a + b. (For, MP = a and NP = b.) It follows that MO + NO = a + b.

A property of touching semicircles - solution

Angles APB and CPD are right because they are subtended by the diameters AB and CD in the two semicircles. It follows that ∠APD = ∠BPC = 90°. These angles are formed by the secants AC and BD and are equal to the half sum of the angular measure of (equal) arcs AC and BD. Each of the arcs, therefore, measures 90°, implying that the central angles AOC and BOD are also right. From here, angles MOB and NOD are complementary: ∠MOB + ∠NOD = 90°; and, since BO = DO, the right triangles CMO and OND are equal. In other words,

MO = DN = b and
NO = BM = a,

while, by the Pythagorean theorem, radius R of (O) equals R = √a² + b². So, for the areas, we get

πa²/2 + πb²/2 = πR²/2,

as required.

Expanding the semicircles to complete circles leads to an additional property:

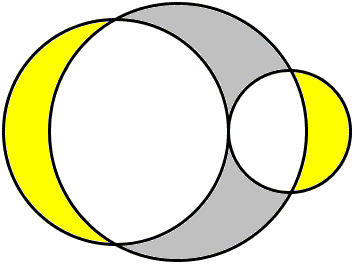
By the Carpet Theorem, the area of an arbelos like gray figures equals the sum of the areas of the two yellow lunes.

Carpets Theorem

71879409

A Property of Semicircles:What is this about? A Mathematical Droodle

Carpets Theorem

A Property of Semicircles:
What is this about?
A Mathematical Droodle