Ptolemy by Inversion

A wonder of wonders: the great Ptolemy's theorem is a consequence (helped by a 19th century invention) of a simple fact that UV + VW = UW, where U, V, W are collinear with V between U and W.

For the reference sake, Ptolemy's theorem reads

Let a convex quadrilateral ABCD be inscribed in a circle. Then the sum of the products of the two pairs of opposite sides equals the product of its two diagonals. In other words,

AD·BC + AB·CD = AC·BD

The 19th century tool we'll use is the inversion. We invert the whole configuration in the circle with center D and (some) radius r:

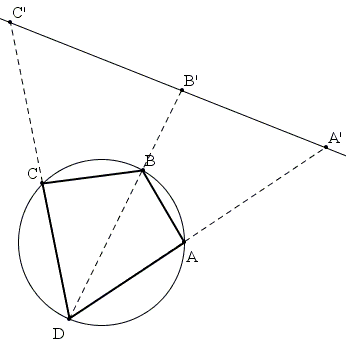
By that inversion, the circumcircle of ABCD maps onto a straight line with images A', B', C', of A, B, C, respectively. For those images we do have A'B' + B'C' = A'C'. At this point we recollect the Angle Preservation Property of the inversion and its consequence - the distance formula:

P'Q' = r2·PQ/(OP·OQ)

that relates the lengths of segments PQ and P'Q' where P' and Q' are inversions of P and Q with center O and radius r.

Applying the distance formula to A'B' + B'C' = A'C' we obtain

A'B' = r2·AB/(DA·DB),
B'C' = r2·BC/(DB·DC),
A'C' = r2·AC/(DA·DC),

which after a substitution and simplification give the required formula

AD·BC + AB·CD = AC·BD.

Remark

Inversion with center D is useful even when the four points A, B, C, D are not concyclic. In that case, of course, points A', B', C' are no longer collinear so that instead of A'B' + B'C' = A'C' we obtain the triangle inequality A'B' + B'C' ≥ A'C'. The same derivation then tells us that in the more general case Ptolemy's equality becomes an inequality

AD·BC + AB·CD ≥ AC·BD.

(A dynamic illustration is available on a separate page.)

References

  1. H. Eves, A Survey of Geometry, Allyn and Bacon, Inc., 1972, p. 132
  2. Liang-shin Hahn, Complex Numbers & Geometry, MAA, 1994, pp. 155-156
  3. A Decade of the Berkeley Mathematical Circle, The American Experience, Volume I, Z. Stankova, Tom Rike (eds), AMS/MSRI, 2008, pp. 17-18
  4. S. E. Louridas, M. Th. Rassias, Problem-Solving and Selected Topics in Euclidean Geometry, Springer, 2013 (48-49)

Ptolemy's Theorem

  1. Ptolemy's Theorem
  2. Sine, Cosine, and Ptolemy's Theorem
  3. Useful Identities Among Complex Numbers
  4. Ptolemy on Hinges
  5. Thébault's Problem III
  6. Van Schooten's and Pompeiu's Theorems
  7. Ptolemy by Inversion
  8. Brahmagupta-Mahavira Identities
  9. Casey's Theorem
  10. Three Points Casey's Theorem
  11. Ptolemy via Cross-Ratio
  12. Ptolemy Theorem - Proof Without Word
  13. Carnot's Theorem from Ptolemy's Theorem

|Contact| |Front page| |Contents| |Geometry| |Up|

Copyright © 1996-2018 Alexander Bogomolny

72352986