Vietnamese Extension of a Japanese Theorem
Problem
Let quadrilateral $ABCD$ be inscribed into circle$(O),$ with center $O,$ with $X,$ $Y,$ $Z,$ $W$ being the midpoints of the corresponding arcs, as shown.
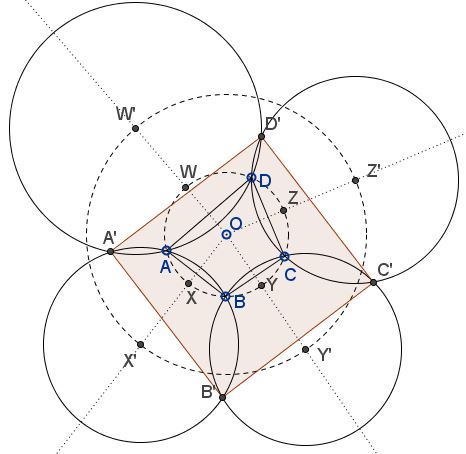
Draw the rays $OX,$ $OY,$ $OZ,$ $OW$ and let $X',$ $Y',$ $Z',$ $W'$ be their intersections with the circle $C(O,R),$ centered at $O$ and with $R$ as the radius. Circles $(ABX'),$ $(BCY'),$ $(C DZ'),$ $( DAW')$ intersect in points $A',$ $B',$ $C',$ $ D'.$
Prove that $A'B'C'D'$ is a rectangle.
Proof 1
As it was shown earlier, when $R$ changes points $A',$ $B',$ $C',$ $D'$ stay on the bisectors of angles $DAB,$ $ABC,$ $BCD,$ and $CDA,$ respectively. These, as we know are parallel to the bisectors of angles $WOX$, $XOY,$ $YOZ,$ $ZOW,$ respectively. This means that, as $R$ changes, the change in the projection, of, say, $W$ on $AA'$ and on $DD'$ are proportional to $\sin\frac{1}{2}\angle WOX$ and $\sin\frac{1}{2}\angle ZOW.$ Denoting these changes $\Delta A$ and $\Delta D$ we have
$\displaystyle\frac{\Delta A}{\Delta D}=\frac{\sin\frac{1}{2}\angle WOX}{\sin\frac{1}{2}\angle ZOW}=const.$
With a reference to (the converse of) Thales' theorem, this allows us to conclude that, as $R$ changes, line $A'D'$ remains parallel to itself. The same holds for the lines $A'B',$ $B'C',$ and $C'D'.$ According to a Japanese Sangaku, when $R$ was equal to the circumradius of $(ABCD),$ points $A'B'C'D'$ formed a rectangle. We may now conclude that it remains a rectangle for all values of $R.$
This is worth observing that the result above is a clear generalization of that sangaku and, thus, serves an additional example where a more general sentence is a consequence of its particular case.
Proof 2
Assume $(ABCD)$ is a unit circle, with center $O$ at the origin. In complex variables, We can then set $A=1,$ $B=e^{2it},$ $C=e^{2iu},$ and $D=e^{2iv},$ where $0\lt t\lt u\lt v\lt\pi.$

Then $X=e^{it},$ $Y=e^{i(t+u)},$ $Z=e^{i(u+v)},$ $W=-e^{iv}.$ By definition, $X'=Re^{it},$ $Y'=Re^{i(t+u)},$ $Z'=Re^{i(u+v)},$ $W'=-Re^{iv}.$
Triangles $AA'X'$ and $AA'W'$ are congruent and inversely oriented, implying,
$\displaystyle \frac{A'-W'}{X'-W'}=\overline{\bigg(\frac{A-W'}{X'-W'}\bigg)}, $
from which we can express $A'=R(e^{it}-e^{iv})+e^{i(t+v)}.$ Similarly, $B'=R(e^{it}+e^{i(t+u)})-e^{iu},$ $C'=R(e^{i(t+u)}+e^{i(u+v)})-e^{i(t+v)},$ and $D'=R(e^{i(u+v)}-e^{iv})+e^{iu}.$ We have
$\begin{align} A'+C' &= \big[R(e^{it}-e^{iv})+e^{i(t+v)}\big]+\big[R(e^{i(t+u)}+e^{i(u+v)})-e^{i(t+v)}\big]\\ &=R(e^{it}-e^{iv})+R(e^{i(t+u)}+e^{i(u+v)})\\ &=\big[R(e^{it}+e^{i(t+u)})-e^{iu}\big]+\big[R(e^{i(u+v)}-e^{iv})+e^{iu}\big]\\ &=B'+D', \end{align}$
which shows that $A'B'C'D'$ is a parallelogram. Further,
$\begin{align} D'-A'&=\big[R(e^{i(u+v)}-e^{iv})+e^{iu}\big]-\big[R(e^{it}-e^{iv})+e^{i(t+v)}\big],\\ &= e^{iv}(R(e^{iu}-e^{it})-(Re^{it}-e^{iu}). \end{align}$
so that $\overline{D'-A'}=-e^{i(t+u+v)}(D'-A').$ Also,
$\begin{align} B'-A'&=\big[R(e^{it}+e^{i(t+u)})-e^{iu}\big]-\big[R(e^{it}-e^{iv})+e^{i(t+v)}\big],\\ &= e^{it}(Re^{iu}-e^{iv})+(Re^{iv}-e^{iu}). \end{align}$
so that $\overline{B'-A'}=e^{i(t+u+v)}(B'-A').$
It follows that
$\displaystyle\frac{D'-A'}{B'-A'}+\overline{\bigg(\frac{D'-A'}{B'-A'}\bigg)}=0,$
implying that $A'B'\perp A'D'.$
Acknowledgment
This is an extension of a Japanese sangaku discovered by Dao Thanh Oai (Vietnam) and posted at the CutTheKNotMath facebook page. The second proof is by Leo Giugiuc (Romania).
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny71546918
