Extras in Bottema's Configuration
What Might This Be About?
Problem 1
Given three squares $BCDE,$ $ABIF,$ and $ACJG,$ the latter two with centers $O$ and $O'.$ Let $P$ be the midpoint of $DG,$ $N$ that of $EF,$ $S$ the intersection of $NO'$ and $OP.$
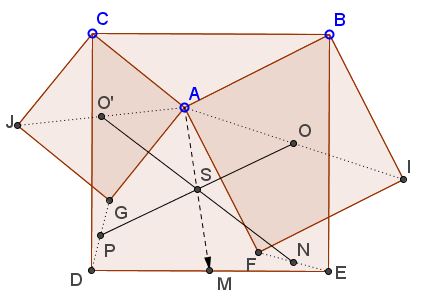
Prove that $AS$ passes through $M,$ the midpoint of $DE.$
Solution
We'll use complex numbers and shall not distinguish between points and the associated complex numbers.
Scaling if necessary, we may define $B=1,$ $C=-1,$ $A=a-bi,$ where are $a,b$ are arbitrary real numbers.
With this, we obtain further values: $D=-1-2i,$ $E=1-2i,$ $M=-2i,$
$\begin{align} G&=i(C-A)+A\\ &=i(-1-a+bi)+(a-bi)\\ &=(a-b)-i(1+a+b). \end{align}$
Similarly,
$\begin{align} F&=-i(B-A)+A\\ &=-i(1-a+bi)+(a-bi)\\ &=(a+b)+i(-1+a-b). \end{align}$
Now we can find all the midpoints:
$\begin{align} O&=\frac{1}{2}(B+F)=\frac{1}{2}[(1+a+b)+i(-1+a-b)],\\ O'&=\frac{1}{2}(C+G)=\frac{1}{2}[(-1+a-b)-i(1+a+b)]. \end{align}$
(Note that $iO'=O.)$ Further,
$\begin{align} P&=\frac{1}{2}(D+G)=\frac{1}{2}[(-1+a-b)-i(-3+a+b)],\\ N&=\frac{1}{2}(E+F)=\frac{1}{2}[(1+a+b)-i(3-a+b)]. \end{align}$
Finally, we'll show that $S$ is the midpoint of both $NO'$ and $OP:$
$\begin{align} \frac{1}{2}(N+O')&=\frac{1}{2}[a-i(2+b)],\\ \frac{1}{2}(O+P)&=\frac{1}{2}[a-i(2+b)], \end{align}$
which proves that $ONGO'$ is a parallelogram. But there is more: $S$ happens to be the midpoint of $A$ and $M.$ Indeed, directly
$\begin{align} \frac{1}{2}(A+M)&=\frac{1}{2}[a-i(2+b)]. \end{align}$
Thus not only $AS$ passes through $M,$ $AM$ is divided by $S$ in half as are $NO'$ and $PO,$ making $AO'PMNO$ a parahexagon.
Note also that $ONGO'$ becomes a rectangle for $A$ on the perpendicular bisector of $BC,$ i.e., when the two small squares are equal. It is a square (equal to the two small squares at that) when $A$ lies on $BC.$
Problem 2
Given two squares $ABIF$ and $ACJG,$ join $I$ and $J,$ and erect perpendiculars to $BC$ at $I,$ $B,$ $C,$ and $J.$ Let $X,Y,U,V$ be the intersections as shown below.
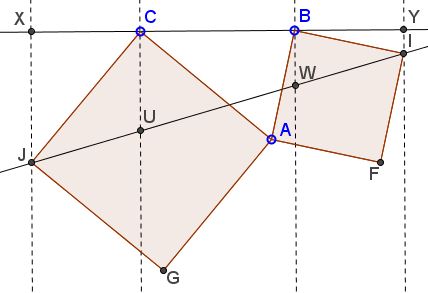
Then $JU=IW.$
Solution
Add a perpendicular to $BC$ through $A:$
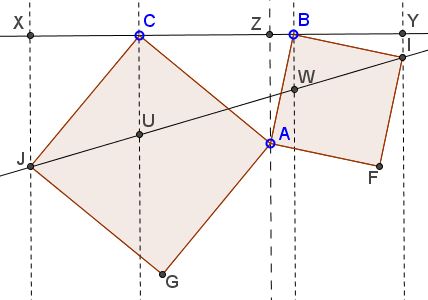
Then $\Delta CJX=\Delta ACZ,$ implying $CX=AZ.$ Also, $\Delta BIY=\Delta ABZ,$ implying $BY=AZ.$ It follows that $BY=CX$ and, therefore, $IW=JU$ as having equal projections on the same line $BC.$
Acknowledgment
The two problems problem which are due to Ruben Dario from the Peru Geometrico group has been communicated to me by Leo Giugiuc. I decided to place them on the same page since both relate to Bottema's theorem. Solution to the first is by Leo Giugiuc.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny71531110
