Midpoint Reciprocity in Napoleon's Configuration
What Might This Be About?
Problem
Let $ABC_{o},$ $BCA_{o},$ $CAB_{o}$ be the outer, $ABC_{i},$ $BCA_{i},$ $CAB_{i}$ the inner Napoleon's triangles.
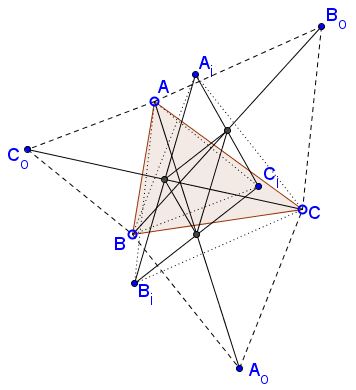
Then the midpoints $AA_{o}$ and $B_{i}C_{i}$ coincide $(A_{m})$ as are the midpoints of $BB_{o},$ $C_{i}A_{i}$ $(B_{m})$ and $CC_{o},$ $A_{i}B_{i}$ $(C_{m}).$ A similar assertion holds with the exchange of the indices $_{o}$ and $_{i}$ throughout.
Proof
We'll use complex numbers. Let $\omega = \cos 60^{\circ}+i\sin 60^{\circ}$ be a counterclockwise rotation through $60^{\circ}.$ Treating points as complex numbers,
$\begin{align} A_{o}&=C+(B-C)\omega\\ B_{i}&=C+(A-C)\omega\\ C_{i}&=A+(B-A)\omega. \end{align}$
so that
$\displaystyle\frac{A+A_{o}}{2}=\frac{(A+C)+(B-C)\omega}{2}.$
Also,
$\displaystyle\frac{B_{i}+C_{i}}{2}=\frac{(A+C)+(B-C)\omega}{2}$
and the proof is complete as other midpoints are treated similarly
Acknowledgment
The statement has been posted by Dao Thanh Oai (Vietnam) at the CutTheKnotMath facebook page.
Napoleon's Theorem
- Napoleon's Theorem
- A proof with complex numbers
- A second proof with complex numbers
- A third proof with complex numbers
- Napoleon's Theorem, Two Simple Proofs
- Napoleon's Theorem via Inscribed Angles
- A Generalization
- Douglas' Generalization
- Napoleon's Propeller
- Napoleon's Theorem by Plane Tessellation
- Fermat's point
- Kiepert's theorem
- Lean Napoleon's Triangles
- Napoleon's Theorem by Transformation
- Napoleon's Theorem via Two Rotations
- Napoleon on Hinges
- Napoleon on Hinges in GeoGebra
- Napoleon's Relatives
- Napoleon-Barlotti Theorem
- Some Properties of Napoleon's Configuration
- Fermat Points and Concurrent Euler Lines I
- Fermat Points and Concurrent Euler Lines II
- Escher's Theorem
- Circle Chains on Napoleon Triangles
- Napoleon's Theorem by Vectors and Trigonometry
- An Extra Triple of Equilateral Triangles for Napoleon
- Joined Common Chords of Napoleon's Circumcircles
- Napoleon's Hexagon
- Fermat's Hexagon
- Lighthouse at Fermat Points
- Midpoint Reciprocity in Napoleon's Configuration
- Another Equilateral Triangle in Napoleon's Configuration
- Yet Another Analytic Proof of Napoleon's Theorem
- Leo Giugiuc's Proof of Napoleon's Theorem
- Gregoie Nicollier's Proof of Napoleon's Theorem
- Fermat Point Several Times Over
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny71547615
