Another Equilateral Triangle in Napoleon's Configuration
What is this about?
A Mathematical Droodle
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
The applet attempts to suggest a problem communicated to me by Marco Antôumflex;nio Manetta at the CutTheKnotMath facebook page:
Form equilateral triangles $ABC'',\;$ $AB''C,\;$ $A''BC\;$ on the sides of $\Delta ABC\;$ and define $D = \frac{1}{2}(A''+B'')\;$ and $E=\frac{1}{2}(A''+C'').$
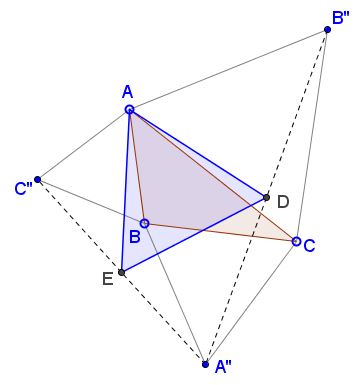
Prove that $\Delta ADE\;$ is equilateral.
Proof 1
We identify the points in the plan with complex numbers. Let $d\;$ be a counterclockwise rotation around origin through $60^{\circ}$ and place the origin at the center of $\Delta ABC.\;$ This implies $A+B+C=0.$
Then the construction is equivalent to the following definitions:
$\displaystyle\begin{align} A''&=C+d(B-C),\\ B''&=A+d(C-A),\\ C''&=B+d(A-B),\\ D&=\frac{A''+B''}{2}=\frac{A+C}{2}+\frac{d}{2}(B-A)=-\frac{B}{2}+\frac{d}{2}(B-A),\\ E&=\frac{A''+C''}{2}=\frac{B+C}{2}+\frac{d}{2}(A-C)=-\frac{A}{2}+\frac{d}{2}(A-C). \end{align}$
What needs to be proved now is
(*)
$d(E-A)=D-A.$
This is reasonably straightforward. We only need to take into account that $d^2-d+1=0.$
$\displaystyle\begin{align} d(E-A) &= d(-\frac{A}{2}+\frac{d}{2}(A-C)-A)\\ &=-\frac{3d}{2}A+\frac{d^2}{2}(A-C)\\ &=-\frac{3d}{2}A+\frac{d-1}{2}(A-C)\\ &=-dA-\frac{d}{2}C-\frac{1}{2}(A-C), \end{align}$
whereas
$\displaystyle\begin{align} D-A &= -\frac{B}{2}+\frac{d}{2}(B-A)-A\\ &=-\frac{C-A}{2}+\frac{d}{2}(B-A). \end{align}$
Thus we need only to compare $\displaystyle -dA-\frac{d}{2}C\;$ and $\displaystyle \frac{d}{2}(B-A),\;$ or $-2A-C$ and $B-A.\;$ The two quantities are equal: $2A+C+B-A=A+B+C=0.\;$
Proof 2
The spectral proof is by Grégoire Nicollier.
Define the three triangle of the Fourier basis: $F_0=(1,1,1),\;$ $F_1=(1,w,w^2)\;$ with $\displaystyle w=e^{2i\frac{\pi}{3}},\;$ $F_2=(1,w^2,w).\;$. The transformation maps $F_0\;$ to $F_0,\;$ $F_1\;$ to $F_2,\;$ and $F_2\;$ to $\frac{1}{2}(F_0+F_2),\;$ leaving the vertex $1\;$ fixed. Thus $\Delta ABC = aF_0 + bF_1 + cF_2\;$ is mapped to $\displaystyle (a+\frac{c}{2})F_0 + (b+\frac{c}{2})F_2,\;$ which is equilateral.
Napoleon's Theorem
- Napoleon's Theorem
- A proof with complex numbers
- A second proof with complex numbers
- A third proof with complex numbers
- Napoleon's Theorem, Two Simple Proofs
- Napoleon's Theorem via Inscribed Angles
- A Generalization
- Douglas' Generalization
- Napoleon's Propeller
- Napoleon's Theorem by Plane Tessellation
- Fermat's point
- Kiepert's theorem
- Lean Napoleon's Triangles
- Napoleon's Theorem by Transformation
- Napoleon's Theorem via Two Rotations
- Napoleon on Hinges
- Napoleon on Hinges in GeoGebra
- Napoleon's Relatives
- Napoleon-Barlotti Theorem
- Some Properties of Napoleon's Configuration
- Fermat Points and Concurrent Euler Lines I
- Fermat Points and Concurrent Euler Lines II
- Escher's Theorem
- Circle Chains on Napoleon Triangles
- Napoleon's Theorem by Vectors and Trigonometry
- An Extra Triple of Equilateral Triangles for Napoleon
- Joined Common Chords of Napoleon's Circumcircles
- Napoleon's Hexagon
- Fermat's Hexagon
- Lighthouse at Fermat Points
- Midpoint Reciprocity in Napoleon's Configuration
- Another Equilateral Triangle in Napoleon's Configuration
- Yet Another Analytic Proof of Napoleon's Theorem
- Leo Giugiuc's Proof of Napoleon's Theorem
- Gregoie Nicollier's Proof of Napoleon's Theorem
- Fermat Point Several Times Over
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
71530217
