Miguel Ochoa's van Schooten Like Theorem III
What Might This Be About?
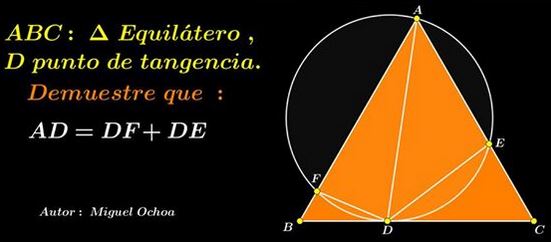
Problem
In $\Delta ABC,$ circle $(O)$ through $A$ and tangent to $BC$ in $D$ cuts $AB$ and $AC$ in $E$ and $F,$ respectively.
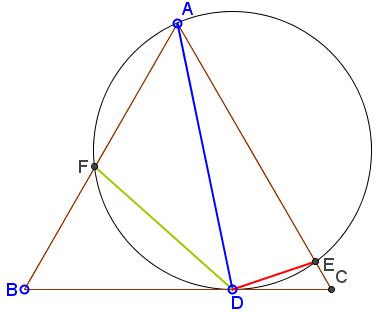
Prove that $DE + DF = AD.$
In the notations I follow the original formulation:
Proof 4
There are two sister pages, one with Proofs 1 and 2 and the other with Proof 3. It seems to me that the present proof due to its elegance deserves to be treated separately.
Let $D'$ be the foot of the altitude from $A.$ Find $E'$ on $AC$ and $F'$ on $AB$ such that $DE'\perp AC$ and $DF'\perp AB.$
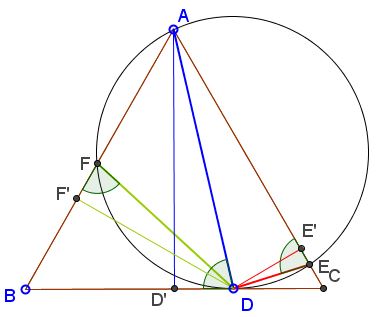
By Viviani's theorem, $AD'=DE'+DF'.$
Next we note that, since $AFDE$ is a cyclic quadrilateral, $\angle DFB=\angle DEA.$ Further, since the circle is tangent to $BC,$ $\angle ADB=\angle DEA.$ Thus, the right triangles $ADD',$ $DEE'$ and $DFF'$ are similar such that $AD'=DE'+DF'$ implies $AD=DE+DF.$
Acknowledgment
The above statement has been posted by Miguel Ochoa Sanchez at the CutTheKnotMath facebook page. The proof is by Gobbalipur Jayanth.
This proof extends to an exciting generalization.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny71536274
