Miguel's Area of Square

What Might This Be About?

Source

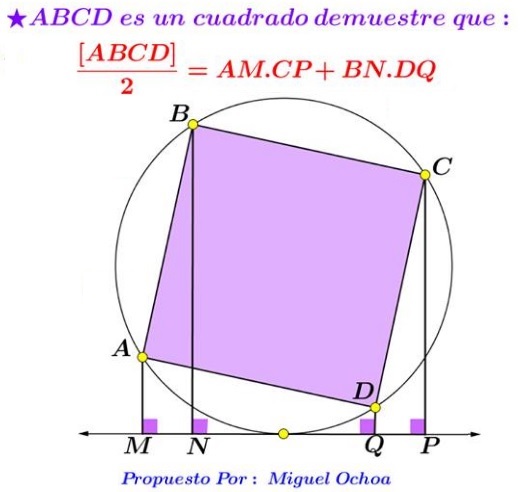
Miguel Ochoa's area of a square, source

Problem

Point $T\;$ is on the circumcircle of square $ABCD.\;$ $AM,\;$ $BN,\;$ $CP,\;$ $DQ\;$ are perpendicular to the tangent to $(ABCD)\;$ at $T.$

Miguel Ochoa's area of a square, problem

Prove that

$\frac{1}{2}[ABCD]=AM\cdot CP+BN\cdot DQ$

where $[ABCD]\;$ is the area of the square $ABCD.$

Proof 1

The proof is based on the following

Lemma

Following the notations in the diagram,

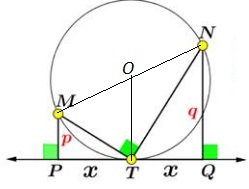
Miguel Ochoa's area of a square, lemma

$x=\sqrt{pq}.$

The lemma follows from the similarity of triangles $MPT\;$ and $TQN.$

From Lemma,

$MT=PT=n=\sqrt{ac},\ NT=QT=m=\sqrt{bd}.$

Using these in the diagram below,

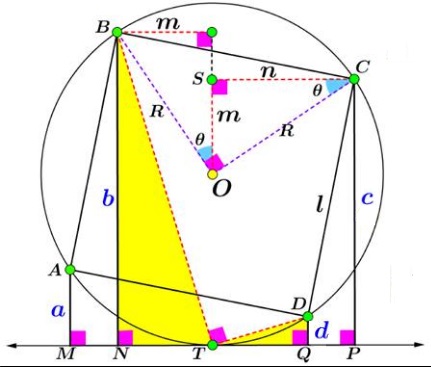
Miguel Ochoa's area of a square, Proof 1

we obtain, by the Pythagorean theorem, $m^2+n^2=R^2,\;$ or, in other words, $\frac{1}{2}\ell^2=ac+bd,\;$ as required.

Proof 2

That is a proof without words, based on the following lemma:

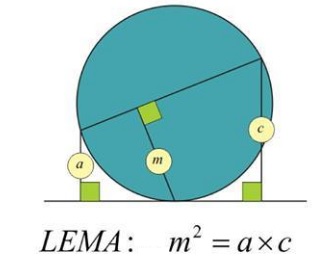
Miguel Ochoa's area of a square, Lemma 2

So in,

Miguel Ochoa's area of a square, Proof 2

$m^2=ac,\;n^2=bd,\;$ and $\frac{1}{2}\ell^2=m^2+n^2=ac+bd.$

Proof 3

Miguel Ochoa's area of a square, Proof 3

Proof 4

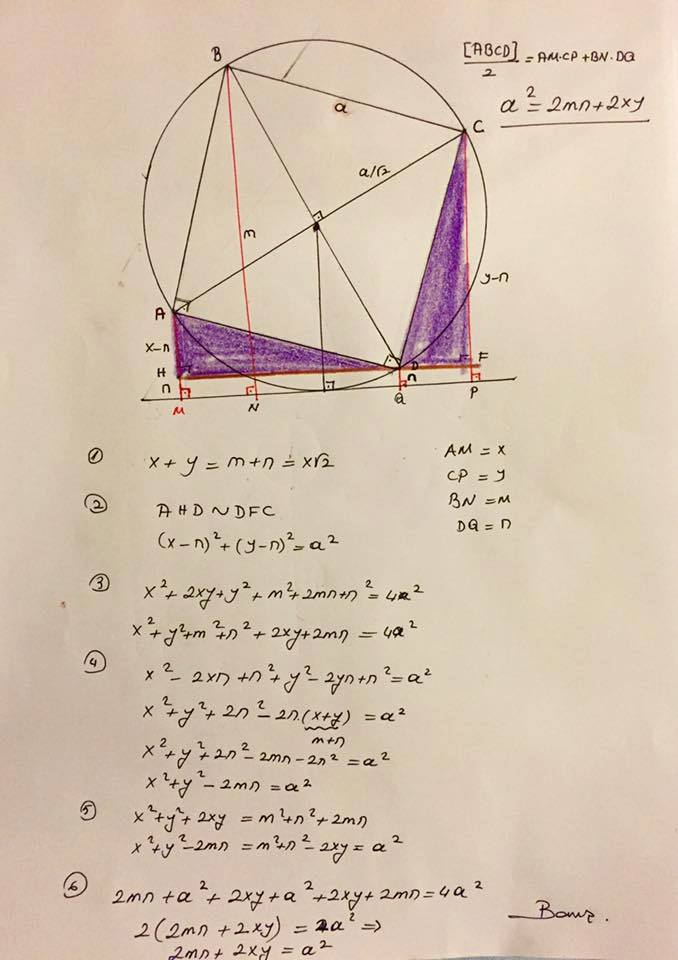
Miguel Ochoa's area of a square, Proof 4

Acknowledgment

The above problem, along with several proofs, has been posted by Miguel Ochoa Sanchez at the CutTheKnotMath facebook page. Proof 1 is by Miguel Ochoa Sanchez; Proof 2 is by Ruben Dario; Proof 3 is by Baris Altay; Proof 4 by Kunihiko Chikaya.

The applet at the beginning of the page may suggest that $AM\cdot CP+BN\cdot DQ\;$ is independent of $T.\;$ With this in mind, it is easy to see that when $T\;$ falls on one of the vertices the result is exactly $\frac{1}{2}[ABCD].\;$ However, when trying to prove the independence from $T\;$ I came up with the proof like that by Kunihiko Chikaya that implies the required result more directly.

72504980