Regular Hexagon and Triangle Joined at Vertex

This is a particular case of the generalized Bottema's theorem.

Let $P$ and $N$ be the midpoints of $AB$ and $A'B,$ respectively.

Chasing angles,

$\begin{align} \angle OPM' &= \angle OPB + \angle BPM'\\ &=90^{\circ}+ (180^{\circ}-\angle PBN = 270^{\circ}-\angle PBN\\ &=360^{\circ}-(60^{\circ}+30^{\circ}+\angle PBN)\\ &=360^{\circ}-(\angle OPB+\angle NBQ^{\circ}+\angle PBN)\\ &=\angle OBQ. \end{align}$

Similarly, $\angle M'NQ=\angle OBQ.$ Further, triangles, $BOP$ and $QBN$ are similar (both are $30-90-60).$ Thus we have a proportion $OP/OB=BN/BQ$ so that $OP/BN=OB/BQ,$ but $BN=PM'$ which, together with $\angle OPM'=\angle OBQ,$ shows that triangles $OPM'$ and $OBQ$ are similar. In the same manner, $\Delta M'NQ\sim\Delta OBQ.$ All this combines to show the following proportions:

$\displaystyle\frac{OP}{OM'}=\frac{M'N}{M'Q}=\frac{BP}{M'Q},$ i.e., $\displaystyle\frac{OP}{BP}=\frac{OM'}{M'Q}.$

and also

$\displaystyle\frac{OP}{OM'}=\frac{OB}{OQ}.$

It follows that $\Delta OBP\sim\Delta OQM',$ such that $\angle OM'Q=\angle OBP=90^{\circ}.$

With apologies, the notations below are somewhat are different from the ones above. Hopefully, this does not make the proof unnecessarily confusing.

Let $E$ and $D$ be the reflections in $M$ of $O_1$ and $B,$ respectively.

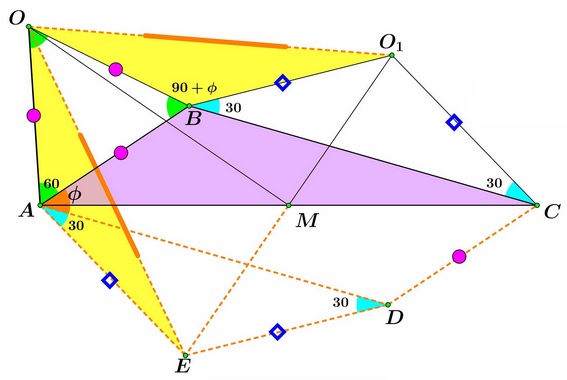
Note that triangles $OAE$ and $OBO_1$ are congruent (SAS), implying $OE=OO_1.$ Then, since $AM=MC,$ $O_1M=ME;$ so in $Delta EOO_1$ $OM$ is an altitude, hence, $\angle OMO_1=90^{\circ}.$