Chain of Four Intersecting Circles

What Might This Be About?

Problem

Circles $(O_{1}),$ $(O_{2}),$ $(O_{3}),$ $(O_{4})$ intersect in points $A_{1},B_{1},$ $A_{2},B_{2},$ $A_{3},B_{3},$ $A_{4},B_{4},$ as shown below.

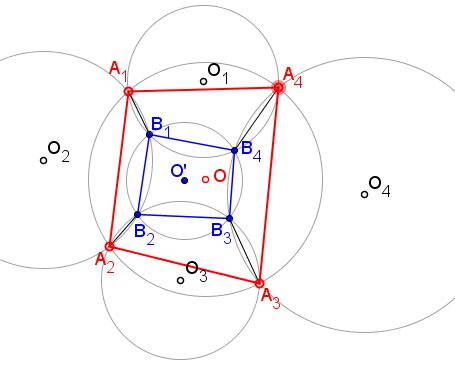
a chain of four intersecting circle - problem

Prove that, if points $A_{1},$ $A_{2},$ $A_{3},$ $A_{4},$ are concyclic, so are points $B_{1},$ $B_{2},$ $B_{3},$ $B_{4}.$

Proof

The problem is solved by pure angle chasing, with repeated application of the fact that in a cyclic quadrilateral the opposite angles add up to $180^{\circ}.$

a chain of four intersecting circle - problem

Indeed,

$A_{2}A_{1}A_{4}+A_{2}A_{3}A_{4}=180^{\circ}\\ (B_{1}A_{1}A_{2}+B_{1}A_{1}A_{4})+(B_{3}A_{3}A_{2}+B_{3}A_{3}A_{4})=180^{\circ},\\ \begin{align} (180^{\circ}-B_{1}B_{2}A_{2})&+(180^{\circ}-B_{1}B_{4}A_{4})+\\ &(180^{\circ}-B_{3}B_{2}A_{2})+(180^{\circ}-B_{3}B_{4}A_{4})=180^{\circ}, \end{align}\\ (B_{1}B_{2}A_{2}+B_{3}B_{2}A_{2})+(B_{3}B_{4}A_{4}+B_{1}B_{4}A_{4})=540^{\circ},\\ B_{1}B_{2}B_{3}+B_{1}B_{4}B_{3}=180^{\circ}.$

Note

A second solution has appeared earlier on a separate page.

71939985