Excircle in Equilateral Triangle
Source
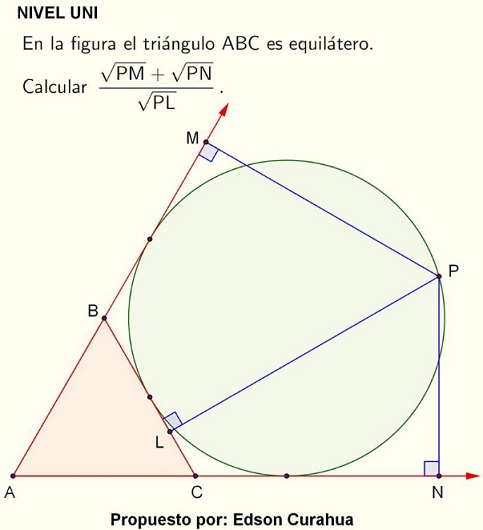
Problem
Point $P\,$ is on the excircle $(O_a)\,$ of $\Delta ABC.\,$ Points $M,N,P\,$ are the projections of $P\,$ on $BC\,$ and on the extensions of $AB\,$ and $AC,\,$ respectively.
Find
$\displaystyle E=\frac{\sqrt{MP}+\sqrt{NP}}{\sqrt{LP}}.$
Solution 1
Choose the circle $x^2+y^2=1.\,$ Since that's the $A\text{-excircle}\,$ of $\Delta ABC,\,$ we'll choose $BC:\,x\sqrt{3}+y=2,\,$ $AC:\,x\sqrt{3}-y+2,\,$ $AB:\,y=-1,\,$ and $P=(\cos t,\sin t),\,$ with $\displaystyle -\frac{\pi}{2}\lt t\lt\frac{5\pi}{6}.$
We get $MP=1+\sin t=1+\cos \left(\frac{\pi}{2}-t\right)=2\cos^2\left(\frac{\pi}{4}-\frac{t}{2}\right),\,$ implying $\sqrt{MP}=\sqrt{2}\displaystyle\cos\left(\frac{\pi}{4}-\frac{t}{2}\right).\,$ Similarly,
$\displaystyle NP=\left|\frac{\sqrt{3}}{2}\cos t-\frac{1}{2}\sin t+1\right|=1+\cos\left(\frac{\pi}{6}+t\right)=2\cos^2\left(\frac{\pi}{12}+\frac{t}{2}\right),$
implying $\displaystyle\sqrt{NP}=\sqrt{2}\cos\left(\frac{\pi}{12}+\frac{t}{2}\right).\,$ Further,
$\displaystyle LP=\left|\frac{\sqrt{3}}{2}\cos t+\frac{1}{2}\sin t+1\right|=1+\cos\left(\frac{\pi}{6}-t\right)=2\cos^2\left(\frac{\pi}{12}-\frac{t}{2}\right),$
implying $\displaystyle\sqrt{LP}=\sqrt{2}\cos\left(\frac{\pi}{12}-\frac{t}{2}\right).\,$ From here,
$\displaystyle\frac{\sqrt{MP}+\sqrt{NP}}{\sqrt{LP}}=\frac{\displaystyle\cos\left(\frac{\pi}{12}+\frac{t}{2}\right)+\cos\left(\frac{\pi}{4}-\frac{t}{2}\right)}{\displaystyle\cos\left(\frac{\pi}{12}-\frac{t}{2}\right)}=\frac{\sqrt{3}\displaystyle\cos\left(\frac{\pi}{12}-\frac{t}{2}\right)}{\displaystyle\cos\left(\frac{\pi}{12}-\frac{t}{2}\right)}=\sqrt{3}.$
Solution 2
In what follows we'll invoke repeatedly the following result from the diagram below.
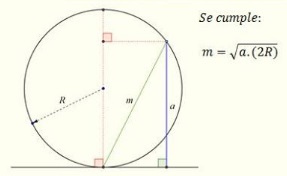
Assuming $R\,$ is the radius of the excircle, we apply the above lemma to three triangles below:
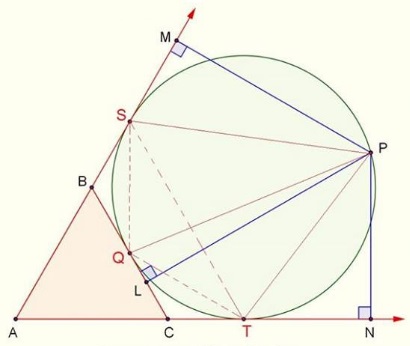
$PS=\sqrt{MP\cdot(2R)},\,$ $PT=\sqrt{NP\cdot(2R)},\,$ $PQ=\sqrt{LP\cdot(2R)}.\,$
$\overparen{SQ}=\overparen{QT}=60^{\circ},\,$ hence, $\overparen{ST}=120^{\circ},\,$ so that $QS=QT=R\,$ and, subsequently, $ST=R\sqrt{3}.$
By Ptolemy's theorem in quadrilateral $QSPT,\,$ $PQ\cdot ST=PT\cdot QS+PS\cdot QT.\,$ A substitution then gives
$\sqrt{LP\cdot (2R)}\cdot R\sqrt{3}=\sqrt{NP\cdot (2R)}\cdot R+\sqrt{MP\cdot ((2R)}\cdot R,$
i.e., $\sqrt{LP}\sqrt{3}=\sqrt{MP}+\sqrt{NP}.$
Acknowledgment
Leo Giugiuc has kindly communicated to me another problem from the peru geometrico facebook group. The problem has been posted by Edson Curahua Ortega, with credits to Edson Curahua. Solution 1 is by Leo Giugiuc; Solution 2 is by John Ascona Briceño.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny71545802
