Equilateral Triangle on Three Lines
What is this about?
Problem
Given three straight lines (denoted below by two points $AB,$ $CD,$ $EF$).
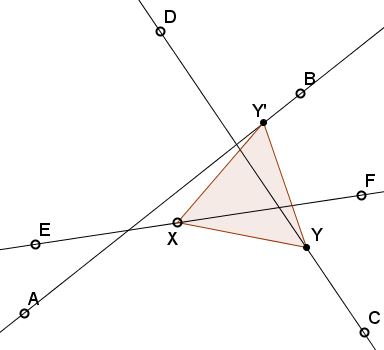
Construct an equilateral triangle with vertices one per line.
Construction
Choose an arbitrary point on one of the line, say $X$ on $EF.$ Rotate $CD$ around $X$ $60^{\circ}$ into $C'D'.$ Let $Y'$ be the intersection of $C'D'$ with $AB$ and $Y$ the point that was mapped into $Y'$ by the rotation.
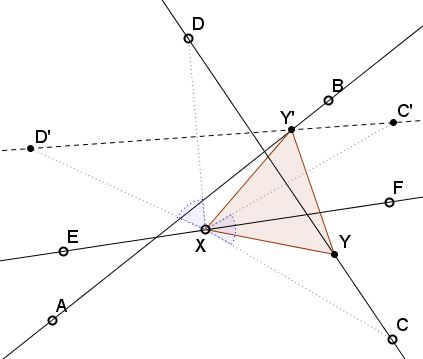
Then $\Delta XYY'$ is equilateral and $X\in EF,$ $Y'\in AB,$ and $Y\in CD.$
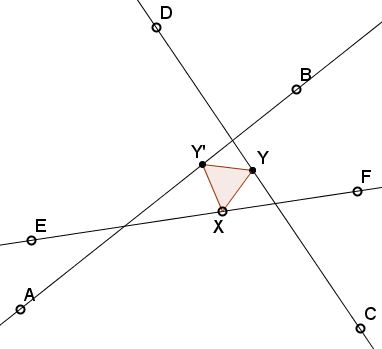
In general, the solution is not unique, e.g.,
Acknowledgment
The construction is classic. For three parallel lines (when the solution is unique up to isomorphism), it can be found in I. M. Yaglom, Geometric Transformations I (MAA, 1962), problem 18. The latter problem has been discussed elsewhere.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny71529317
