A Generalization of Van Aubel's Theorem
What Is It About?
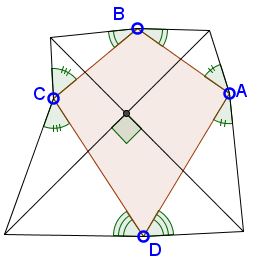
Problem
The applet purports to illustrate the following statement:
If one erects right-hand ears on the sides of the quadrilateral $(z_0,\,z_1,\,z_2,\,z_3)\;$ with ear angles $\alpha$ at $z_0,\;$ $\beta$ at $z_1,\;$ $\frac\pi2-\alpha\;$ at $z_2,\;$ and $\frac\pi2-\beta\;$ at $z_3,\;$ the segments joining the opposite ear apices are perpendicular.
Proof 1
The triangle $(0,\,1,\,Z(\alpha,\,\beta))\;$ of the upper half plane with angles $\alpha\;$ at $1\;$ and $\beta\;$ at $0\;$ is given by
$\displaystyle Z(\alpha,\,\beta)=\frac{\tan\alpha}{\tan\alpha+\tan\beta}(1 +i\tan\beta).$
The apex of the ear erected on the side $z_0\rightarrow z_1\;$ is $z_1 + (z_0 - z_1)\cdot Z(\alpha,\beta)\;$. The quotient of the vectors joining the opposite ear apices is thus
$\displaystyle\frac{z_3 + (z_2 - z_3)\cdot Z(\pi/2 -\alpha,\,\pi/2 -\beta) - \left[z_1 + (z_0 - z_1)\cdot Z(\alpha,\,\beta)\right]}{z_0 + (z_3 - z_0)\cdot Z(\pi/2 -\beta,\,\alpha) - \left[z_2 + (z_1 - z_2)\cdot Z(\beta, \,\pi/2 -\alpha)\right]},$
which simplifies to
$\displaystyle-i\frac{1+\tan\alpha\tan\beta}{\tan\alpha+\tan\beta}.$
Remark
Observe that the final formula,
$\displaystyle-i\frac{1+\tan\alpha\tan\beta}{\tan\alpha+\tan\beta}$
is independent of the quadrilateral and, for $\alpha=\beta=45^{\circ},\;$ the ratio is $-i\;$ and its absolute value $1,\;$ as expected. This is also true for the left-hand ears, with the analogous formula obtained when the triangle $(0,\,1,\,Z(\alpha,\,\beta))\;$ is replaced with $(0,\,1,\,\overline{Z}(\alpha,\,\beta)).\;$
Proof 2
For the basis quadrilaterals $(1,0,0,0),\;$ $(0,1,0,0),\;$ $(0,0,1,0),\;$ and $(0,0,0,1)\;$ it is easy to see with a figure and the sine law that the vectors joining the opposite ear apices are always at right angles with the same orientation and with length ratio $\displaystyle\frac{\cos (\alpha-\beta)}{\sin(\alpha+\beta)}.\;$ As these vectors are linear functions of the vertices, the vectors joining the opposite ear apices for any quadrilateral are also at right angles with the same orientation and length ratio.
Acknowledgment
The statement is by Oai Thanh Dào; both proofs and the remark are due to Grégoire Nicollier.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny71546537
