Circle in Isosceles Triangle and a Fixed Point
What is this about?
Problem
$P$ and $Q$ are points on the equal sides $AB$ and $AC,$ respectively, of an isosceles $\Delta ABC$ such that $AP = CQ.$ Moreover, neither $P$ nor $Q$ is a vertex of $\Delta ABC.$
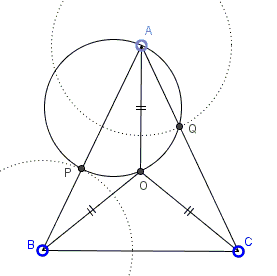
Prove that the circumcircle of $\Delta APQ$ passes through the circumcenter of $\Delta ABC.$
Hint
This page lists five different solutions and there is a sixth one elsewhere. It is hard to choose one "the most natural or enlightening" to point you to. The problem is not difficult; just give it a shot.
Solution 1
Let in the complex plane $A(2i),$ $B(-2b),$ $C(2b),$ where $b=\cot B.$ This implies that the circumcenter of $\Delta ABC$ is $O((1-b^2)\cdot i$ and that there is $m\in(0,1)$ such that $P=(-2b\cdot (1-m)+2i\cdot m)$ and $Q=(2b\cdot m+2i\cdot (1-m))$. The points $A,$ $P,$ $Q$ and $O$ are concyclic if only if their harmonic ratio is real. Let's check:
$\begin{align}\displaystyle\frac{P-A}{Q-A}:\frac{P-O}{Q-O}&=\frac{-2(1-m)(b+i)}{2m(b-i)}\cdot\frac{2mb+(1-2m+b^{2})\cdot i}{-2(1-m)b+(-1+2m+b^{2})\cdot i}\\ &=\frac{m-1}{m}\in\mathbb{R}. \end{align}$
Q.E.D.
Solution 2
Let in the complex plane, $A(-1),$ $B(e^{-2it}),$ and $C(2^{2it}),$ where $t\in (0,\pi/2).$ Then the circumcenter is the origin and there is $m\in (0,1)$ such that $P=(-(1-m)+me^{-2it})$ and $Q=(-m+(1-m)e^{2it}).$ The fact that $\frac{P-A}{Q-A}:\frac{P-O}{Q-O}\in\mathbb{R}$ is immediate.
Solution 3
Let $w$ be the circumcircle of $\Delta ABC.$ $P$ and $Q$ are on sides $AB$ and $AC,$ meaning they inside $w.$ Let $p$ be the power of $P$ relative to $w,$ $q$ that of $Q.$ Then
$p=PA\cdot PB=QC\cdot QA=q.$
But $p=R^{2}-PO^{2},$ where $R$ is the circumradius of $\Delta ABC;$ similarly, $q=R^{2}-QO^{2},$ implying $PO=QO.$
Next we observe that in case $P$ and $Q$ are the midpoints of $AB$ and $AC$ the solution is trivial, $PQA$ being an isosceles triangle. So, assume $P$ and $Q$ are not the midpoints of $AB$ and $AC.$ Then in $\Delta AOP,$ $AO/\sin\angle APO=PO/\sin(A/2).$ In $\Delta AOQ,$ $AO/\sin\angle AQO=QO/\sin(A/2),$ such that $\sin\angle APO=\sin\angle AQO.$ But the two angles are clearly not equal, so they are supplementary, making the four points $A,P,O,Q$ concyclic.
Solution 4
Assume without loss of generality that $AP\gt AQ$ and that $M$ is the midpoint of $AC.$ Let $PS\parallel BC$ with $S\in AC.$ $OM\perp QS,$ so $OQ=OS,$ but $OP=OS,$ implying that $O$ is the circumcenter of $\Delta PQS.$
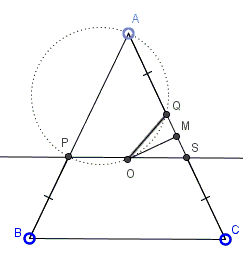
Further, $\angle PSQ=\angle ACB,$ making $\angle POQ=2\angle ACB,$ such that $\angle BAC+\angle POQ=180^{\circ}.$
Solution 5
Assume $O$ is the circumcenter of $\Delta ABC.$
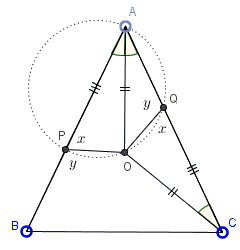
Then $OA=OC$ and, by construction, $AO=CQ.$ Also, $\angle OCA=\angle OAC=\angle OAP,$ making $\Delta COQ=\Delta AOP$ by SAS; similarly, $\Delta BOP=\Delta AOQ.$ It follows $\angle OQC=\angle OPA=x$ and $\angle OPB=\angle OQA=y.$ But $x+y=180^{\circ}.$ Therefore, $O$ lies on the circumcircle of $A,P,Q.$
Acknowledgment
The five solutions on this page have been communicated to me by Leonard Giugiuc from Romania who wrote, "The fifth solution belongs to Constantin Guigiuc, my father, a great math teacher. It was also discovered by Diana Trailescu, my beloved girlfriend, which is math teacher, too." There is also a sixth solution.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny71546561
