Camouflaged Butterfly
Source
Leo Giugiuc has kindly posted at the CutTheKnotMath facebook page a problem due to Miguel Ochoa Sanchez:
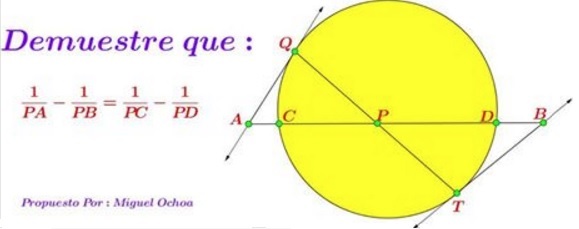
Problem
Chord $CD\;$ and $QT\;$ of a given circle meet at point $P.\;$ The tangents at $Q\;$ and $T\;$ cross $CD\;$ extended at $A\;$ and $B,\;$ respectively.
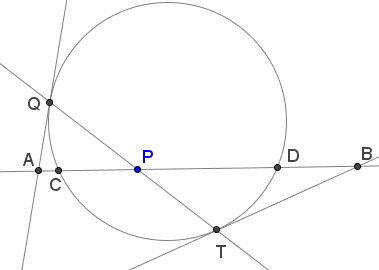
Prove that $\displaystyle\frac{1}{AP}-\frac{1}{BP}=\frac{1}{CP}-\frac{1}{DP}.$
Solution 1
By the Power of a Point Theorem, $AC\cdot AD=AQ^2,\;$ $BD\cdot BC=BT^2,\;$ and $CP\cdot DP=PQ\cdot PT,\;$ implying $(AC(AP+DP)=AQ^2\;$ and $BD(BP+CP)=BT^2.\;$ By Stewart's theorem in $\Delta QAP\;$ for the cevian $QC,$
$CQ^2\cdot AP+AC\cdot AP\cdot CP=PQ^2\cdot AC+AQ^2\cdot CP,$
so that $CQ^2\cdot AP+AC\cdot AP\cdot CP=PQ^2\cdot AC+AC(AP+DP)\cdot CP,\quad$ or $CQ^2\cdot AP=PQ^2\cdot AC+AC\cdot CP\cdot DP,\;$ or else, $CQ^2\cdot AP=PQ^2\cdot AC+AC\cdot PQ\cdot PT,\;$ and, finally, $CQ^2\cdot AP=AC\cdot PQ\cdot PT.\;$ Similarly, $DT^2\cdot BP=BD\cdot PT\cdot QT.$
We thus have $\displaystyle\frac{QC^2}{DT^2}=\frac{BP\cdot AC\cdot PQ}{AP\cdot BD\cdot PT}.\;$ But triangles $PCQ\;$ and $PTD\;$ are similar, so that $\displaystyle\frac{QC^2}{DT^2}=\frac{PQ^2}{DP^2},\;$ or $\displaystyle\frac{PQ^2}{DP^2}=\frac{BP\cdot AC\cdot PQ}{AP\cdot BD\cdot PT},\;$ implying $\displaystyle\frac{1}{DP^2}=\frac{BP\cdot AC}{AP\cdot BD\cdot PT\cdot PQ},\;$ or $\displaystyle\frac{1}{DP^2}=\frac{BP\cdot AC}{AP\cdot BD\cdot CP\cdot DP}.\;$ Simplifying, $\displaystyle\frac{AP\cdot CP}{BP\cdot DP}=\frac{AC}{BD},\;$ i.e., $\displaystyle\frac{AP\cdot CP}{BP\cdot DP}=\frac{AP-CP}{BP-DP},\;$ which is $\displaystyle\frac{BP-DP}{BP\cdot DP}=\frac{AP-CP}{AP\cdot CP},\;$ or $\displaystyle\frac{1}{DP}-\frac{1}{BP}=\frac{1}{CP}-\frac{1}{AP},\;$ as required.
Solution 2
Draw $AQ\parallel BS.\;$ We'll use the notations as defined in the diagram below:
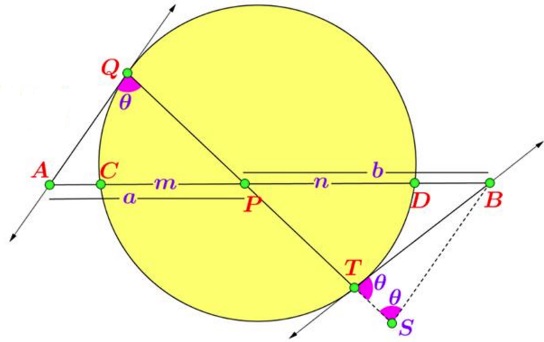
We have $\displaystyle\frac{a}{b}=\frac{AO}{BS}=\frac{AQ}{BT}.\;$ From this
$\displaystyle\left(\frac{a}{b}\right)^2=\left(\frac{AQ}{BT}\right)^2=\frac{AD\cdot AC}{BC\cdot BD}=\frac{(a+n)(a-m)}{(b+m)(b-n)},$
From this we deduce
$\displaystyle\frac{(a+n)(a-m)}{a^2}=\frac{(b+m)(b-n)}{b^2},$
which is the same as $\displaystyle\frac{1}{a}-\frac{1}{b}=\frac{1}{m}-\frac{1}{n},\;$ as required.
Remark
The problem above is a clear generalization of the one, Butterfly in Inscriptible Quadrilateral. Furthermore, the genuine Butterfly Theorem in which the fact that $P\;$ is the midpoint of one of the segments, $AB,\;$ $CD,\;$ implies its being the midpoint of the other, has been generalized to exactly same condition $\displaystyle\frac{1}{DP}-\frac{1}{BP}=\frac{1}{CP}-\frac{1}{AP},\;$ for an arbitrary $P,\;$ see, e.g., the remark at the end of Proof 8 of the Butterfly Theorem.
Acknowledgment
Solution 1 is by Leo Giugiuc and Dan Sitaru; Solution 2 is by Miguel Ochoa Sanchez.
Butterfly Theorem and Variants
- Butterfly theorem
- 2N-Wing Butterfly Theorem
- Better Butterfly Theorem
- Butterflies in Ellipse
- Butterflies in Hyperbola
- Butterflies in Quadrilaterals and Elsewhere
- Pinning Butterfly on Radical Axes
- Shearing Butterflies in Quadrilaterals
- The Plain Butterfly Theorem
- Two Butterflies Theorem
- Two Butterflies Theorem II
- Two Butterflies Theorem III
- Algebraic proof of the theorem of butterflies in quadrilaterals
- William Wallace's Proof of the Butterfly Theorem
- Butterfly theorem, a Projective Proof
- Areal Butterflies
- Butterflies in Similar Co-axial Conics
- Butterfly Trigonometry
- Butterfly in Kite
- Butterfly with Menelaus
- William Wallace's 1803 Statement of the Butterfly Theorem
- Butterfly in Inscriptible Quadrilateral
- Camouflaged Butterfly
- General Butterfly in Pictures
- Butterfly via Ceva
- Butterfly via the Scale Factor of the Wings
- Butterfly by Midline
- Stathis Koutras' Butterfly
- The Lepidoptera of the Circles
- The Lepidoptera of the Quadrilateral
- The Lepidoptera of the Quadrilateral II
- The Lepidoptera of the Triangle
- Two Butterflies Theorem as a Porism of Cyclic Quadrilaterals
- Two Butterfly Theorems by Sidney Kung
- Butterfly in Complex Numbers
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny71537138
