Batman's Problem

What Might This Be About?

Problem

A quadrilateral $ABCD\;$ is inscribed in a circle with center $O.\;$ Its diagonals meet at $M.\;$ The circumcircle of $ABM\;$ intersect the sides $AD\;$ and $BC\;$ at $N\;$ and $K,\;$ respectively.

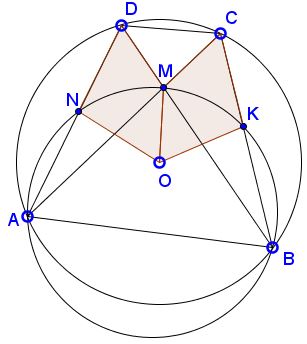
Batman's Problem - problem

Prove that the areas of the convex quadrilaterals $NOMD\;$ and $KOMC\;$ are equal.

Solution

Inscribed angles $CAD\;$ and $CBD\;$ are equal, implying that $\angle MAN=\angle KBM\;$ which, as inscribed into $(AMB),\;$ are then subtended by equal chords: $KM=MN.\;$

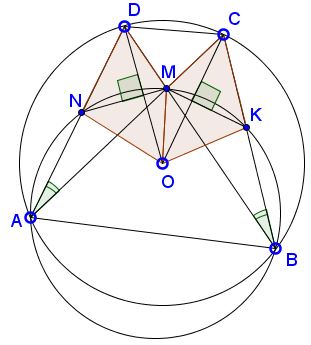
Batman's Problem - solution

In addition, $NM\;$ is an antiparallel in $\Delta ABD,$ so that $MN\perp OD.\;$ Similarly, $KM\perp OC.\;$ If $[F]\;$ designates the area of shape $F\;$ then

$[NOMD]=\frac{1}{2}OD\cdot MN=\frac{1}{2}OC\cdot KM=[KOMC].$

Acknowledgment

The problem that is due to Emil Stoyanov who posted it at the CutTheKnotMath facebook page. The problem has been offered earlier at the XII Zhautykov Olympiad.

Related material
Read more...

  • What Is Antiparallel?
  • Antiparallel via Three Reflections
  • Symmedian and Antiparallel
  • Tucker Circles
  • Symmedian and 2 Antiparallels
  • Circle through the Incenter And Antiparallels
  • Antiparallel and Circumradius

    • |Contact| |Front page| |Contents| |Geometry|

    Copyright © 1996-2018 Alexander Bogomolny

    71862825