A Triangle With a 45 Degrees Angle in Square
What Is This About?
Problem
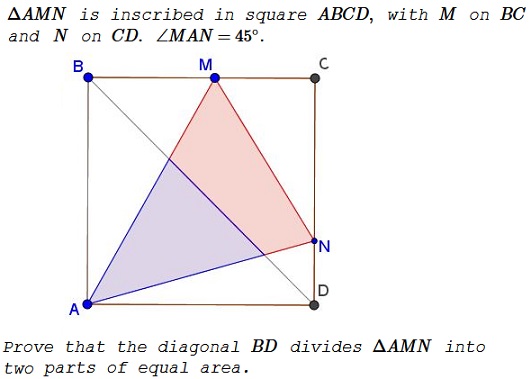
Solution 1
Thinking in terms of paper folding, fold $\Delta ABM\,$ over $AM\,$ and $\Delta ADN\,$ over $AN.\,$ Note that $\angle BAM+\angle DAN=45^{\circ}=\angle MAN.\,$ It follows that the edges $AB\,$ and $AD\,$ of the folded triangles will coincide. If $L\,$ is their common endpoint then $\angle ALM=\angle ALN=90^{\circ}\,$ so that $L\,$ lies on $MN\,$ and $AL\perp MN.\,$ $AL\,$ is an altitude in $\Delta MAN.$
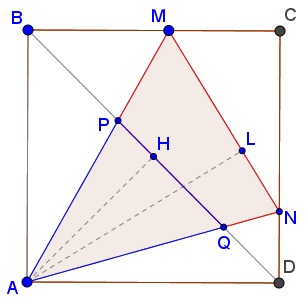
The folding argument shows that $\angle AND=\angle ANL\,$ (and, in passing, $\angle AMB=\angle AML.)\,$ Since $\angle DQN=\angle AQP\,$ and $\angle MAN=45^{\circ}=\angle NDQ,\,$ triangles $DNQ\,$ and $APQ\,$ are similar, implying $\angle APQ=\angle AND=\angle ANM.\,$ Thus triangles $AQP\,$ and $AMN\,$ are similar. Their areas relate as the square of any pair of their corresponding linear elements. Now, assuming $AL=AB=1,\,$ $AH=\displaystyle\frac{\sqrt{2}}{2},\,$ making $[\Delta AMN]=2[\Delta AQP]\,$ and, consequently, $[\Delta AQP]=[MNQP],\,$ as required.
Solution 2
Let $P$ and $Q$ be the points where $AN$ and $AM$ intersect the diagonal $BD,$ respectively. It is noted that $\angle QAN=\angle QDN= 45^{\circ}.$ Thus, $AQND$ is a cyclic quadrilateral, therefore implying that $\angle AQN=90^{\circ}.$
This in turn implies that $\Delta AQN$ is a right-isoceles triangle with $AN$ as the hypotenuse. Thus, $\displaystyle AQ=\frac{AN}{\sqrt{2}}.$
The same argument can be employed to show that $\displaystyle AP=\frac{AM}{\sqrt{2}}.$
Now, since triangles $APQ$ and $AMN$ share a common vertex angle $A,$ we have, $\displaystyle \frac{Area(\Delta APQ)}{Area(\Delta AMN)}=\frac{AQ\cdot AP}{AM\cdot AN}.$ However, from the conclusions in the previous two paragraphs, we have $\displaystyle \frac{AQ}{AN}=\frac{AP}{AM}=\frac{1}{\sqrt{2}}$.
This therefore implies that $\displaystyle \frac{Area(\Delta APQ)}{Area(\Delta AMN)}=\frac{1}{2},$ or equivalently, $\displaystyle \frac{Area(\Delta APQ)}{Area(MNPQ)}=1,$ as claimed by the problem.
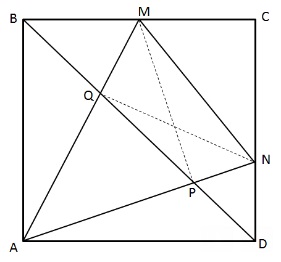
Extra properties of the configuration
This problem is a converse of the one discussed earlier. The configuration is rich with various properties; some of these could be inferred from the following diagram:
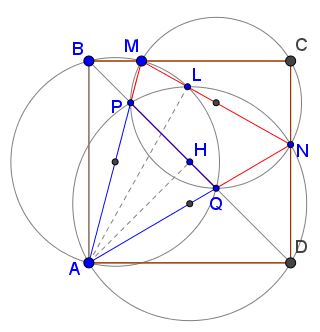
An extra problem
Below, the areas of the blue and red regions are equal.
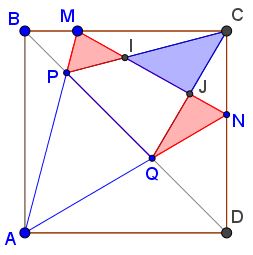
This is a direct application of Carpets Theorem. It can be easily verified that $\angle PCQ=45^{\circ},\,$ which shows that $[MNQP]=[\Delta AQP]=[\Delta CPQ].\,$ If so, by removing the common part - $IJQP\,$ - from $\Delta CPQ\,$ and the quadrilateral $MNQP\,$ gives the required result.
Generalization
$\Delta AMN$ is inscribed in a quadrilateral $ABCD$ where $BC=CD,$ with $M$ on $BC$ and $N$ on $CD,$ such that $\angle MAN=\angle CBD[=\theta].$ The diagonal $BD$ intersects triangle $AMN$ at $P$ and $Q.$ Show that the diagonal $BD$ dissects $\Delta AMN$ into two areas, whose ratio is a constant, i.e., $\displaystyle \frac{Area(\Delta APQ)}{Area(MNPQ)}$ is constant.
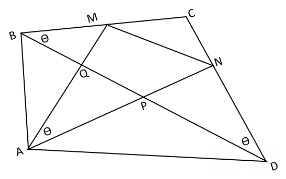
For a proof, note that $\angle QAN=\angle QDN=\theta.$ Thus, $AQND$ is a cyclic quadrilateral, therefore implying that $\angle AQN= 180^{\circ}-\angle ADC.$ This implies that the angles of $\Delta AQN$ are independent of the specific position of $M$ or $N,$ and thus, $\displaystyle \frac{AQ}{AN}=c_1,$ a constant.
Similarly, $ABMP$ is a cyclic quadrilateral and $\angle APM=180^{\circ}-\angle ABC.$ Thus, again the angles of $\Delta AMP$ are independent of the specific position of $M$ or $N,$ and thus, $\displaystyle \frac{AP}{AM}=c_2,$ a constant.
Now, since triangles $APQ$ and $AMN$ share a common vertex angle $A,$ we have, $\displaystyle \frac{Area(\Delta APQ)}{Area(\Delta AMN)}=\frac{AQ\cdot AP}{AM\cdot AN}=c1\cdot c2=constant.$ Finally, $\displaystyle \frac{Area(\Delta APQ)}{Area(\Delta MNPQ}= \frac{c1\cdot c2}{1- c1\cdot c2}$ another constant, as claimed by the generalization.
Acknowledgment
The problem, due to V. Proizvolov, appeared in Kvant - a popular Russian magazine - (#1, 2004, M1895), with a solution in a later issue (#4, 2004).
The extra properties and the extra problem have been suggested by Bariş Altay (Turkey). Solution 2 and the generalization are by G. S. Ranganath and his son G. R. Jayanth.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny71533939
