Integer Triangles with Two Angles in the Ratio 1 : 2
Problem
Construct an integer-sided triangle $ABC,$ with $\gamma =2\alpha,$ where, as usual, $\alpha=\angle BAC,$ $\beta=\angle ABC.$
The applet below illustates the construction.
Construction
Given $\alpha\in\left(0^\circ,60^\circ\right)$, we construct a triangle $ABC$ with $\gamma=2\alpha$. (One has then $\beta>\gamma>\alpha$ for $\alpha<36^\circ$, $\gamma>\beta>\alpha$ for $36^\circ<\alpha<45^\circ$, and $\gamma>\alpha>\beta$ for $\alpha>45^\circ$.) We obtain a simpler proof of the results of [Willson and Luthar].
Erect on the base side $c=AB$ with midpoint $M$ the isosceles triangle $ABC'$ with base angles $\alpha$ and the right-angled triangle $ABC''$ with hypotenuse $AB$ and angle $\alpha$ at $A$. $C$ is the reflection of $C'$ in $C''$
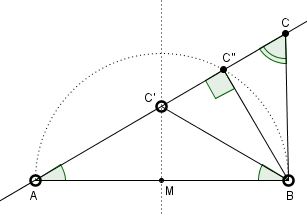
Simple angle chasing shows that $\gamma=2\alpha$. The side $a$ is also the leg of the isosceles triangle $ABC'$: the range of $a=c/(2\cos\alpha)$ is $(c/2,c)$. The similar right-angled triangles $AMC'$ and $AC''B$ give $\displaystyle \frac{c/2}a=\frac{b-x}c$, where $x$ denotes $C''C$ if $\alpha<45^\circ$ and $-C''C$ if $\alpha>45^\circ$. Thus $\displaystyle b-x=\frac{c^2}{2a}$ and $\displaystyle b=2(b-x)-a=\frac{c^2}a-a$, that is, $c^2=a(a+b)$.
Theorem
The numbers $a$, $b$, $c$ are the sides of a triangle with $\gamma=2\alpha$ if and only if $c\gt 0$, $c/2\lt a\lt c$, and $\displaystyle b=\frac{c^2}{a}-a$. The change from $\beta\gt \gamma$ to $\beta\lt\gamma$ occurs for $b=c$ at $\displaystyle a=\frac{\sqrt{5}-1}{2}c$ (with $\displaystyle\cos 36^{\circ}=\frac{\sqrt{5}+1}{4}$ as a consequence), the change from $\beta\gt\alpha$ to $\beta\lt\alpha$ at $a=c/\sqrt{2}$.
Consider such a triangle with integer coprime sides $a$ and $b$ ($a$ and $a+b$ are then also coprime). Since $c^2=a(a+b)$, $c$ is an integer if and only if $a$ and $a+b$ are squares: $a=n^2$, $a+b=m^2$, $b=m^2-n^2$, $c=mn$. (If $a$, $b$, $c$ are integers with $c^2=a(a+b)$, each common divisor of $a$ and $b$ divides $c$.)
Theorem
The integers $a$, $b$, $c$ with greatest common divisor $1$ are the sides of a triangle with $\gamma=2\alpha$ if and only if $a=n^2$, $b=m^2-n^2$, and $c=mn$ for coprime integers $n$, $m$ with $1\leq n\lt m\lt 2n$.
For example, $n=2$, $m=3$: $a=4$, $b=5$, $c=6$; $n=3$, $m=4$: $9$, $7$, $12$; $n=3$, $m=5$: $9$, $16$, $15$. One has $\displaystyle\cos\alpha=\frac{m}{2n}$ by the Law of Cosines.
References
Aknowledgement
The construction, the proof, and the references have been communicated by Grégoire Nicollier (University of Applied Sciences of Western Switzerland) in private correspondence.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny71534527
