Dorin Marghidanu's Tribute to Descartes
Source

Problem
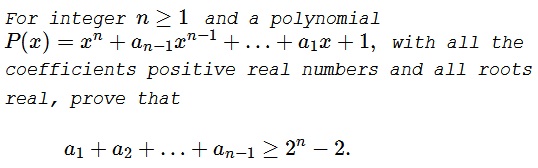
Solution 1
Due to Descartes' Rule of Signs, all roots of the polynomial are nonpositive. Assume these are $-x_k,\,$ $k=1,\ldots,n,\,$ with all $x_k\ge 0.\,$ Since, by Viète's formulas, $\displaystyle \prod_{k=1}^nx_k=1,\,$ the all $x_k\gt 0.\,$ By the AM-GM inequality,
$\displaystyle P(1)=\prod_{k=1}^n(1+x_k)\ge\prod_{k=1}^n(2\sqrt{x_k})=2^n\sqrt{\prod_{k=1}^nx_k}=2^n.$
But $P(1)=2+\displaystyle \sum_{k=1}^{n-1}a_k,\,$ thus proving the result.
Solution 2
Due to Descartes' Rule of Signs, all roots of the polynomial are negative. Let these be $-x_k,\,$ $k=1,\ldots,n,\,$ with all $x_k\gt 0.\,$ Thus,
(1)
$P(x)=(x+x_1)(x+x_2)\cdot\ldots\cdot(x+x_n).$
Using Viète's relations
(2)
$\displaystyle x_1\cdot x_2\cdot\ldots\cdot x_{n}=1.$
With the AM-GM inequality,
(3)
$\displaystyle k+x_i=\underbrace{1+\ldots+1}_{\text{k times}}+x_i\ge (k+1)\sqrt[k+1]{x_i}.$
Putting together (1) and (3),
(4)
$\displaystyle P(k)=\prod_{i=1}^n(k+x_i)\ge (k+1)^n\sqrt[k+1]{x_1\cdot\ldots\cdot x_n}=(k+1)^n.$
Letting in (4) $k=1\,$ delivers the result.
Solution 3
We'll invoke a corollary of the Binomial Theorem,
$\displaystyle {n\choose 0}+{n\choose 1}+\ldots+{n\choose n}=2^n.$
Let $-x_i,\,$ $x_i\gt 0,\,$ $i=1,\ldots,n,\,$ be the roots of the polynomial. $x_1\cdot\ldots\cdot x_n=1.\,$ Further, Using Viète's relations, and the AM-GM inequality,
$\displaystyle \begin{align} &a_{n-1}=\sum_{i=1}^nx_i\ge{n\choose 1}\sqrt[{n\choose 1}]{\prod_{i=1}^nx_i}={n\choose 1}\\ &a_{n-2}=\sum_{i=1,j=1}^nx_ix_j\ge{n\choose 2}\sqrt[{n\choose 2}]{\prod_{i=1,j=1}^nx_ix_j}={n\choose 2}\\ &\qquad\qquad\cdots\cdots\\ &a_{1}=\sum x_{i_1}x_{i_2}\cdot\ldots\cdot x_{i_{n-1}}\ge{n\choose n-1}\sqrt[{n\choose n-1}]{\prod_{i=1}^n x_{i_1}x_{i_2}\cdot\ldots\cdot x_{i_{n-1}}}={n\choose n-1}. \end{align}$
Summing up and using the corollary of the Binomial Theorem we mentioned at the outset gives the desired inequality.
Acknowledgment
This problem has been kindly posted at the CutTheKnotMath facebook page by Dorin Marghidanu. Solution 1 is by Leo Giugiuc; Solution 2 is Dorin Marghidanu; Solution 3 is by Vaggelis Stamatiadis.
![]()
|Contact| |Up| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny71535099