Kunihiko Chikaya's Inequality with a Constraint
Problem
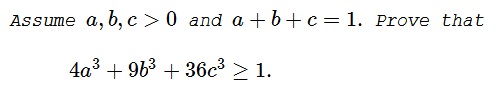
Solution 1
$\displaystyle \begin{align} 4a^3-3a+1=(a+1)(2a-1)^2\ge 0,\\ 9b^3-3b+\frac{2}{3}=\left(b+\frac{2}{3}\right)(3b-1)^2\ge 0,\\ 36c^3-3c+\frac{1}{3}=\left(c+\frac{1}{3}\right)(6c-1)^2\ge 0. \end{align}$
Summing up,
$\displaystyle\begin{align} 4a^3+9b^3+36c^3&\ge 3(a+b+c)-\left(1+\frac{2}{3}+\frac{1}{3}\right)\\ &=3\cdot 1-2=1. \end{align}$
Solution 2
The required inequality is a special case of the following statement:
Assume $x+y+z=1$ and $a+b+c=1,$ $a,b,c,x,y,z \gt 0.$ Then
$\displaystyle \frac{a^3}{x^2} + \frac{b^3}{y^2} + \frac{c^3}{z^2} \ge 1.$
Indeed, by Radon's inequality,
$\displaystyle \frac{a^3}{x^2} + \frac{b^3}{y^2} + \frac{c^3}{z^2}\ge\frac{(a+b+c)^3}{(x+y+z)^2} = 1.$
In this problem $\displaystyle x=\frac{1}{2},$ $\displaystyle y=\frac{1}{3},$ $\displaystyle z=\frac{1}{6}.$
Solution 3
Obviously $\displaystyle \frac{\frac{a}{3}+\frac{a}{3}+\frac{a}{3}+\frac{b}{2}+\frac{b}{2}+c}{6} = \frac{1}{6}.$ By the power-mean theorem
$\displaystyle\begin{align} \frac{3\left(\frac{a}{3}\right)^3 +2\left(\frac{b}{2}\right)^3 + c^3}{6} &\ge\left(\frac{3\frac{a}{3}+2\frac{b}{2}+c}{6}\right)^3\\ &=\left(\frac{1}{6}\right)^3. \end{align}$
Multiplying both parts by $6^3$ yields the required result.
Solution 4
$\displaystyle \begin{align} a&=\frac{4}{3}\cdot 3\cdot \frac{1}{2}\cdot \frac{1}{2}\cdot a\le\frac{4}{3}\left(\frac{1}{8}+\frac{1}{8}+a^3\right)=\frac{1}{3}+\frac{4}{3}a^3\\ b&=3\cdot 3\cdot \frac{1}{3}\cdot \frac{1}{3}\cdot b\le 3\left(\frac{1}{27}+\frac{1}{27}+b^3\right)=\frac{2}{9}+3b^3\\ c&=12\cdot 3\cdot \frac{1}{6}\cdot \frac{1}{6}\cdot c\le 12\left(\frac{1}{216}+\frac{1}{216}+c^3\right)=\frac{1}{9}+12c^3 \end{align}$
Summing up,
$\displaystyle 1=a+b+c\le\frac{2}{3}+\frac{4}{3}a^3+3b^3+12c^3,$
i.e.,
$\displaystyle 1=3\left(1-\frac{2}{3}\right)\le 4a^3+9b^3+36c^3.$
Solution 5
The function $v=y^3$ is convex, so that by Jensen's inequality,
$\displaystyle \begin{align} 4a^3+9b^3+36c^3 &= \frac{1}{2}(2a)^3+\frac{1}{3}(3b)^3+\frac{1}{6}(6c)^3\\ &\ge\left( \frac{1}{2}(2a)+\frac{1}{3}(3b)+\frac{1}{6}(6c)\right)^3\\ &=(a+b+c)^3=1. \end{align}$
Solution 6
We can eyeball from the constraint of the Lagrangian that $3\cdot 4a^2=3\cdot 9b^2=3\cdot 36c^2,$ giving the minimum of $4a^3+9b^3+36c^3$ at $\displaystyle (a,b,c)=\left(\frac{1}{2},\frac{1}{3},\frac{1}{6}\right).$ We know it is a minimum because the second derivatives are $24a,54b, 216c$ are all positive and the Lagrangian has no cross terms.
Acknowledgment
Kunihiko Chikaya has shared his inequality, along with a solution of his at the mathematical inequalities facebook group. Both were first posted on the web on September 13, 2014. I am grateful to Kunihiko for the permission to reproduce his post here.
Solution 2 is by Konstantin Knop; Solution 3 is by Maxim Razin; Solution 4 is by Tran Quoc Thinh; Solution 6 is by N. N. Taleb.
Inequalities with the Sum of Variables as a Constraint
- An Inequality for Grade 8 $\left(\displaystyle\frac{1-x_1}{1+x_1}\cdot\frac{1-x_2}{1+x_2}\cdot\ldots\cdot\frac{1-x_n}{1+x_n}\ge\frac{1}{3}\right)$
- An Inequality with Constraint $((x+1)(y+1)(z+1)\ge 4xyz)$
- An Inequality with Constraints II $\left(\displaystyle abc+\frac{2}{ab+bc+ca}=p+\frac{2}{q}\ge q-2+\frac{2}{q}\right)$
- An Inequality with Constraint V $\left(\displaystyle\prod_{k=1}^{n}x_k^{1/x_k}\le \frac{1}{n^{n^2}}\right)$
- An Inequality with Constraint VI $\left(\displaystyle\prod_{k=1}^{n}\frac{1+x_k}{x_k}\ge \prod_{k=1}^{n}\frac{n-x_k}{1-x_k}\right)$
- An Inequality with Constraint XI $(\sqrt{5a+4}+\sqrt{5b+4}+\sqrt{5c+4} \ge 7)$
- Monthly Problem 11199 $\left(\displaystyle\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge\frac{25}{1+48abc}\right)$
- Problem 11804 from the AMM $(10|x^3 + y^3 + z^3 - 1| \le 9|x^5 + y^5 + z^5 - 1|)$
- Sladjan Stankovik's Inequality With Constraint $\left(abc+bcd+cda+dab-abcd\le\displaystyle \frac{27}{16}\right)$
- Sladjan Stankovik's Inequality With Constraint II $(a^4+b^4+c^4+d^2+4abcd\ge 8)$
- An Inequality with Constraint V $\left(\displaystyle\prod_{k=1}^{n}x_k^{1/x_k}\le \frac{1}{n^{n^2}}\right)$
- An Inequality with Constraint VI $\left(\displaystyle\prod_{k=1}^{n}\frac{1+x_k}{x_k}\ge \prod_{k=1}^{n}\frac{n-x_k}{1-x_k}\right)$
- An Inequality with Constraint XII $(abcd\ge ab+bc+cd+da+ac+bd-5)$
- An Inequality with Constraint XIII $((3a-bc)(3b-ca)(3c-ab)\le 8a^2b^2c^2)$
- Inequalities with Constraint XV and XVI $\left(\displaystyle\frac{a^2}{\sqrt{b^2+4}}+\frac{b^2}{\sqrt{c^2+4}}+\frac{c^2}{\sqrt{a^2+4}}\gt\frac{3}{5}\right)$ and $\left(\displaystyle\frac{a^2}{\sqrt{b^4+4}}+\frac{b^2}{\sqrt{c^4+4}}+\frac{c^2}{\sqrt{a^4+4}}\gt\frac{3}{5}\right)$
- An Inequality with Constraint XVII $(a^3+b^3+c^3\ge 0)$
- An Inequality with Constraint in Four Variables $\left(\displaystyle\frac{a^3}{b+c}+\frac{b^3}{c+d}+\frac{c^3}{d+a}+\frac{d^3}{a+b}\ge\frac{1}{8}\right)$
- An Inequality with Constraint in Four Variables II $(a^3+b^3+c^3+d^3 + 6abcd \ge 10)$
- An Inequality with Constraint in Four Variables III $\left(\displaystyle\small{abcd+\frac{15}{2(ab+ac+ad+bc+bd+cd)}\ge\frac{9}{a^2+b^2+c^2+d^2}}\right)$
- An Inequality with Constraint in Four Variables IV $\left(\displaystyle 27+3(abc+bcd+cda+dab)\ge\sum_{cycl}a^3+54\sqrt{abcd}\right)$
- Inequality with Constraint from Dan Sitaru's Math Phenomenon $\left(\displaystyle b+2a+20\ge 2\sum_{cycl}\frac{a^2+ab+b^2}{a+b}\ge b+2c+20\right)$
- An Inequality with a Parameter and a Constraint $\left(\displaystyle a^4+b^4+c^4+\lambda abc\le\frac{\lambda +1}{27}\right)$
- Cyclic Inequality with Square Roots And Absolute Values $\left(\displaystyle \prod_{cycl}\left(\sqrt{a-a^2}+\frac{1}{2\sqrt{2}}|3a-1|\right)\ge\frac{1}{6\sqrt{6}}\prod_{cycl}\left(\sqrt{a}+\frac{1}{\sqrt{3}}\right)\right)$
- From Six Variables to Four - It's All the Same $\left(\displaystyle \frac{5}{2}\le a^2+b^2+c^2+d^2\le 5\right)$
- Michael Rozenberg's Inequality in Three Variables with Constraints $\left(\displaystyle 4\sum_{cycl}ab(a^2+b^2)\ge\sum_{cycl}a^4+5\sum_{cycl}a^2b^2+2abc\sum_{cycl}a\right)$
- Michael Rozenberg's Inequality in Two Variables $\left(\displaystyle \sqrt{x^2+3}+\sqrt{y^2+3}+\sqrt{xy+3}\ge 6\right)$
- Dan Sitaru's Cyclic Inequality in Three Variables II $\left(\displaystyle \sum_{cycl}\sqrt{1+\frac{1}{a^2}+\frac{1}{(a+1)^2}}\geq \frac{9}{12-2(ab+bc+ca)}+3\right)$
- Dan Sitaru's Cyclic Inequality in Three Variables IV $\left(\displaystyle \sum_{cycl}\frac{(x+y)z}{\sqrt{4x^2+xy+4y^2}}\le 2\right)$
- Dan Sitaru's Cyclic Inequality in Three Variables VI $\left(\displaystyle \sum_{cycl}\left[\sqrt{a(a+2b)}+\sqrt{b(b+2a)}\,\right]\le 6\sqrt{3}\right)$
- An Inequality with Arbitrary Roots $\left(\displaystyle \sum_{cycl}\left(\sqrt[n]{a+\sqrt[n]{a}}+\sqrt[n]{a-\sqrt[n]{a}}\right)\lt 18\right)$
- Inequality 101 from the Cyclic Inequalities Marathon $\left(\displaystyle \sum_{cycl}\frac{c^5}{(a+1)(b+1)}\ge\frac{1}{144}\right)$
- Sladjan Stankovik's Inequality With Constraint II $(a^4+b^4+c^4+d^2+4abcd\ge 8)$
- An Inequality with Constraint in Four Variables $\left(\displaystyle\frac{a^3}{b+c}+\frac{b^3}{c+d}+\frac{c^3}{d+a}+\frac{d^3}{a+b}\ge\frac{1}{8}\right)$
- An Inequality with Constraint in Four Variables IV $\left(\displaystyle 27+3(abc+bcd+cda+dab)\ge\sum_{cycl}a^3+54\sqrt{abcd}\right)$
- Cyclic Inequality with Square Roots And Absolute Values $\left(\displaystyle \prod_{cycl}\left(\sqrt{a-a^2}+\frac{1}{2\sqrt{2}}|3a-1|\right)\ge\frac{1}{6\sqrt{6}}\prod_{cycl}\left(\sqrt{a}+\frac{1}{\sqrt{3}}\right)\right)$
- From Six Variables to Four - It's All the Same $\left(\displaystyle \frac{5}{2}\le a^2+b^2+c^2+d^2\le 5\right)$
- Michael Rozenberg's Inequality in Two Variables $(\displaystyle \sqrt{x^2+3}+\sqrt{y^2+3}+\sqrt{xy+3}\ge 6)$
- Dan Sitaru's Cyclic Inequality in Three Variables II $\left(\displaystyle \sum_{cycl}\sqrt{1+\frac{1}{a^2}+\frac{1}{(a+1)^2}}\geq \frac{9}{12-2(ab+bc+ca)}+3\right)$
- Dorin Marghidanu's Two-Sided Inequality $\left(\displaystyle \small{64(a+bc)(b+ca)(c+ab)}\le \small{8(1-a^2)(1-b^2)(1-c^2)}\le \small{(1+a)^2(1+b)^2(1+c^2)}\right)$
- Problem 6 from Dan Sitaru's Algebraic Phenomenon $(x\sqrt{y+1}+y\sqrt{z+1}+z\sqrt{x+1}\le 2\sqrt{3})$
- A Warmup Inequality from Vasile Cirtoaje $\left(a^4b^4+b^4c^4+c^4a^4\le 3\right)$
- An Extension of the AM-GM Inequality $\left(x_{1}x_{2} + x_{2}x_{3} + x_{3}x_{4} + \ldots + x_{99}x_{100} \le \frac{1}{4}\right)$
- An Extension of the AM-GM Inequality: A second look $\left(x_{1}x_{2} + x_{2}x_{3} + x_{3}x_{4} + \ldots + x_{n-1}x_{n} \le \frac{a^2}{4}\right)$
- Distance Inequality $\left(a^2+b^2+c^2\le\displaystyle\frac{9}{2}\right)$
- Kunihiko Chikaya's Inequality with a Constraint An Inequality with Five Variables, Only Three Cyclic $\left(\displaystyle \left(a+\frac{b}{c}\right)^4+ \left(a+\frac{b}{d}\right)^4+ \left(a+\frac{b}{e}\right)^4\ge 3(a+3b)^4\right)$
- Second Pair of Twin Inequalities: Twin 1 $\left(\displaystyle \prod_{i=1}^n\left(\frac{1}{a_i^2}-1\right)\ge (n^2-1)^n\right)$
- Second Pair of Twin Inequalities: Twin 2 $\left(\displaystyle \prod_{i=1}^n\left(\frac{1}{a_i}+1\right)\ge (n+1)^{n}\right)$
- Cyclic Inequality In Three Variables from the 2018 Romanian Olympiad, Grade 9 $\left(\displaystyle \frac{a-1}{b+1}+\frac{b-1}{c+1}+\frac{c-1}{a+1}\ge 0\right)$
- Dan Sitaru's Cyclic Inequality in Three Variables IX $\left(\displaystyle \sum_{cycl}\sqrt{(x+y+1)(y+z+1)}\le 6+\sum_{cycl}\frac{x^3+y^3}{x^2+y^2}\right)$
- Vasile Cirtoaje's Cyclic Inequality with Three Variables $\left(\displaystyle \sqrt{\frac{a}{b+c}}+\sqrt{\frac{b}{c+a}}+\sqrt{\frac{c}{a+b}}\ge 2\right)$ Leo Giugiuc and Vasile Cirtoaje's Cyclic Inequality $\left(\displaystyle \sqrt{\frac{a}{1-a}}+\sqrt{\frac{b}{1-b}}+\sqrt{\frac{c}{1-c}}+\sqrt{\frac{d}{1-d}}\ge 2\right)$
![]()
|Contact| |Up| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny71536238