Golden Ratio in an Irregular Pentagon

Here is a curious problem with a surprising solution [Prasolov, #4.9, p. 77, pp. 85-86]:

In a pentagon ABCDE the diagonals cut off triangles of area 1. Find the area of the pentagon.

(I thank Bui Quang Tuan for bringing this reference to my attention.)

References

V. V. Prasolov, Problems in Planimetry, v 1, Nauka, Moscow, 1986 (Russian)

Solution

Golden Ratio in an Irregular Pentagon

In a pentagon ABCDE the diagonals cut off triangles of area 1. Find the area of the pentagon.

Pentagons with the given property have diagonals parallel to the sides. We prove this first and then show that the points of intersection of the diagonals divide each in the golden ratio.

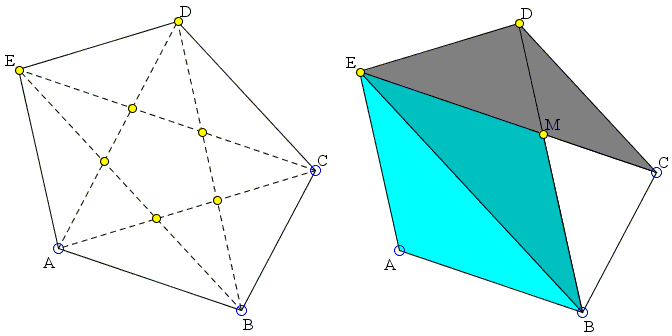
First note that, since triangles ABC and ABE have the same area, the altitudes from C and E to AB must be equal so that CE||AB. The same holds for other pairs side/diagonal.

Let M be the point of intersection of BD and CE. Then ABME is a parallelogram and ΔABE = ΔMEB. Denote Area(BCM) = x. Then

Area(ABCDE) = Area(ABE) + Area(MEB) + Area(DEC) + x = 3 + x.

On the other hand,

(*)	Area(BCM) / Area(CDM) = BM / DM = Area(MEB) / Area(DEM),

Observe that, since BCDE is a trapezoid, Area(DEM) = Area(BCM) = x. So that, in terms of x, (*) looks like

x / (1 - x) = 1 / x,

which gives an equation for x: x² + x - 1 = 0. It follows that x = (√5 - 1)/2 implying BM/DM = φ, the golden ratio. It follows that

Area(ABCDE) = 3 + (√5 - 1)/2 = (√5 + 5)/2.

Bui Quang Tuan gave a practical Euclidean construction of such pentagons. He also observed that the pentagon formed by the diagonals is of the same kind. We may add that, if the sides of the pentagon are extended to form a star whose vertices constitute another such pentagon.

Finally, there is an additional construction of those pentagons.

Fibonacci Numbers

Golden Ratio in Geometry

71546476