Golden Ratio and Midpoints

In a 2011 article, Jo Niemeyer, offered an elegant way of constructing the Golden Ratio with three equal segments, their midpoints and a pair of perpendicular lines.

Three equal segments A1B1, A2B2, A3B3 are positioned in such a way that the endpoints B2, B3 are the midpoints of A1B1, A2B2 respectively, while the endpoints A1, A2, A3 are on a line perpendicular to A1B1.

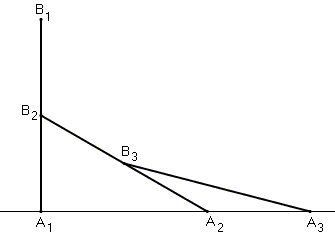
In this arrangement, A2 divides A1A3 in the golden ratio, namely, A1A3 / A1A2 = φ.

For a proof, drop a perpendicular B3H from B3 to A1A2.

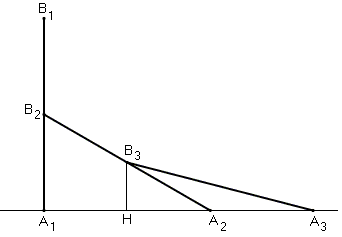
Assume for convenience that all three line segments are of length 2. Then in right triangle A3B3H, A3B3 = 2, and B3H = 1/2 (as a midline in ΔA1A2B2).

By the Pythagorean theorem,

(A3H)² = (A3B3)² - (B3H)² = 4 - 1/4 = 15/4,

so that A3H = √15/2.

On the other hand, in right triangle A1A2B2, A2B2 = 2, and A1B2 = 1, making A1A2 = √3 and A1H = √3/2.

It follows that A1A3 = A1H + A3H = √3(√5 + 1)/2, and, finally, A1A3 / A1A2 = [√3(√5 + 1)/2] / √3 = φ.

References

  1. Jo Niemeyer, A Simple Construction of the Golden Section, Forum Geometricorum, Volume 11 (2011) 53

Fibonacci Numbers

  1. Ceva's Theorem: A Matter of Appreciation
  2. When the Counting Gets Tough, the Tough Count on Mathematics
  3. I. Sharygin's Problem of Criminal Ministers
  4. Single Pile Games
  5. Take-Away Games
  6. Number 8 Is Interesting
  7. Curry's Paradox
  8. A Problem in Checker-Jumping
  9. Fibonacci's Quickies
  10. Fibonacci Numbers in Equilateral Triangle
  11. Binet's Formula by Inducion
  12. Binet's Formula via Generating Functions
  13. Generating Functions from Recurrences
  14. Cassini's Identity
  15. Fibonacci Idendtities with Matrices
  16. GCD of Fibonacci Numbers
  17. Binet's Formula with Cosines
  18. Lame's Theorem - First Application of Fibonacci Numbers

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

72104506