Yet Another Appearance of the Golden Ratio
The Golden ratio made yet another appearance in a geometric configuration. At this point, this appears to be a neusis construction. It would be interesting to investigate if it could be performed with compass and ruler.
However, there are several ways to establish the fact of the Golden ratio presence. These are indicated in the diagram below. I may be missing something; for, at the source reference, the explanation is rather casual.
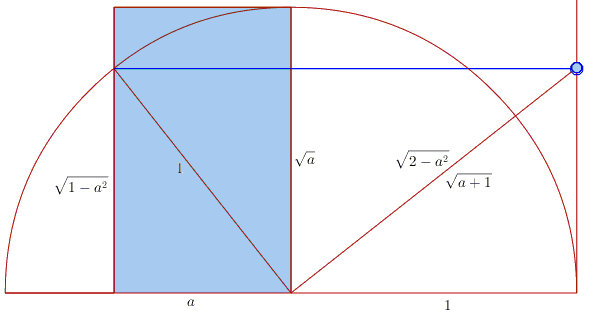
The diagram depicts a few segment lengths obtained with the Pythagorean theorem.
The altitude of a right triangle is a geometric mean of the pieces of the hypotenuse on both sides of its foot: $\sqrt{a}=\sqrt{1-a^2}.$ Squaring and rearranging leads to $a^2+a-1=0,$ with two roots: $1/\phi$ and $-\phi.$
The area of a right triangle can be compute as half the product of its legs or half the product of the hypotenuse by the altitude: $\sqrt{a+1}=(a+1)\sqrt{a}$, and also $(a+1)\sqrt{1-a^2}=1\cdot \sqrt{2-a^2}.$ The former leads to $(a+2)(a^2+a-1)=0,$ the latter to $(a^2+a-1)^2=0.$
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny71534678
