Stern-Brocot Tree

The Stern-Brocot tree is built with the mediant fractions. Place two starting terms 0/1 and 1/0 some way apart and their mediant fraction 1/1 in between and a little down. This creates two gaps: one between 0/1 and 1/1 and another between 1/1 and 1/0. Compute two corresponding mediants and place them below 1/1. Continue in this manner. The next step will add a row of four fractions, then 8, and so on.

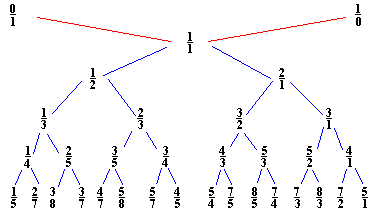
Stern-Brocot tree

It's a remarkable property of the Stern-Brocot tree that the mediant fractions obtained in that manner always come out in lowest terms. The fact is proven by induction based on the following property of the tree: any two fractions m₁/n₁ and m₂/n₂ whose mediants may be computed at any stage of the construction, satisfy

(1)

m₂n₁ - m₁n₂ = 1

A mediant fraction generated by two terms that satisfy (1) stands in the same relation with both of its progenitors. From here we observe that the rows of numerators and denominators of the terms in the Stern-Brocot tree are computed independently of each other. They may be dealt with separately. The row of numerators starts with the pair of integers 0,1. The row of denominators starts with the pair of integers 1,0. They are just symmetric reflections of each other. Let denote the first tree as [0, 1] and the second [1, 0]. We may generalize and consider trees that grow from an arbitrary pair of integers [x,y].

Since, at any stage of construction, we only carry out linear operations (actually only addition), we get a whole vector space of trees. The space is 2-dimensional as we can write [x,y] = x[1,0] + [0,1]. Each tree [x,y] consists of two parts: the left tree [x,x+y] =x[1,1] + y[0,1] and the right tree [x+y,y] = x[1,0] + y[1,1]. The tree [1,1] is a mirror image of itself. In particular, all its rows are palindromic.

Let's record several observations:

The tree of the denominators [1,0] has [1,1] as its left part.
The left part of the tree of the numerators [0,1] is still [0,1] while [1,1] is now the right part.
Fractions on the left from 1/1 are less than 1; fractions on the right from 1/1 are greater than 1

Combining all together we see that

The left part of the tree of the denominators is palindromic.
The right part of any row of numerators coincides with the left part of the corresponding row of denominators.
The left part of the row of numerators coincides with the previous row of numerators.

Surprisingly, the Stern-Brocot tree contains all non-negative fractions. Therefore, its left subtree contains all fractions between 0 and 1. Somehow it must be possible to pluck off the tree the Farey series of any order. Whatever the exact process, since the only criteria for selecting a fraction into the series is the magnitude of its denominator, and, as we know, the right part of any row of denominators is palindromic, the same will always be true for the denominators in the Farey series.

Pick's Theorem

71546648