Tangents And Bisectors

Here's a problem by Miguel Ochoa Sanchez with a solution by Claudia Nanuti, Diana Trailescu, Dan Sitaru and Leo Giugiuc posted at the CutTheKnotMath facebook page:

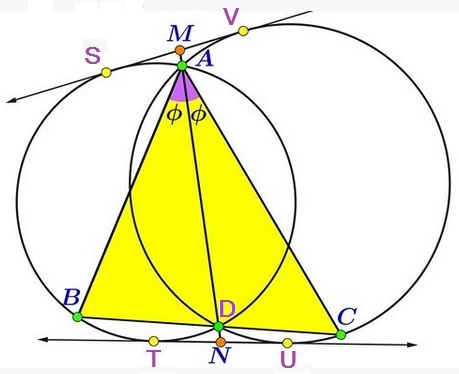
Tangents And Bisectors- problem

Prove that $MN=\sqrt{AB\cdot AC}.$

Proof

From the symmetry in the line of the centers $TU=SV$ and $MA=ND.$ In addition, the fact that $M$ and $N$ lie on the radical axis of the two circles makes them the midpoints of $SV$ and $TU,$ respectively.

Now, by the Power of a point theorem, $ND\cdot NA=\frac{1}{4}TU^{2}$ and $MD\cdot MA=\frac{1}{4}SV^{2}.$

Further, $MN=AD+MA+ND=AD+2ND$ such that $ND=\frac{1}{2}(MN-AD)$ while $MN+AD=2NA$ such that $NA=\frac{1}{2}(MN+AD).$ Thus we see that

$\displaystyle\frac{MN-AD}{2}\cdot\frac{MN+AD}{2}=\frac{TU^{2}}{4}.$

In other words, $MN^{2}=AD^{2}+TU^{2}.$

Let $O$ be the center of $(ABD),$ $Q$ the center of $(ACD).$

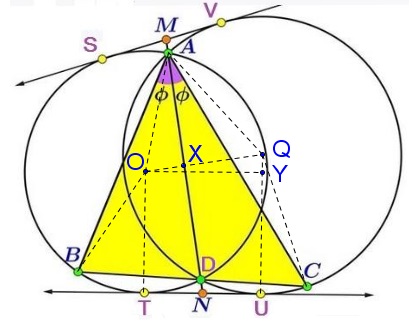
Tangents And Bisectors- solution

Now, triangles $ABC$ and $AOQ$ are similar. Indeed,

$\angle AOQ =\frac{1}{2}\angle AOD = \angle ABD = \angle ABC.$

Similarly, $\angle AQO=\angle ACB.$

In $(ABD),$ $\angle AOB=2\angle ADB$ so that in $\Delta AOB,$

$\begin{align} \angle BAO&=\frac{1}{2}(\pi -\angle AOB)\\ &=\frac{1}{2}(\pi-2\angle ADB)\\ &=\frac{1}{2}\pi-(\pi-\angle B-\frac{1}{2}\angle A)\\ &=\angle B+\phi-\frac{1}{2}\pi \end{align}$

and

$\displaystyle AO=\frac{AB}{2\sin\angle ADB}=\frac{AB}{2\sin (\angle B+\phi)}.$

From the similarity of triangles $ABC$ and $AOQ,$ $\displaystyle AQ=\frac{AC}{2\sin (\angle B+\phi)}$ and $\displaystyle OQ=\frac{BC}{2\sin (\angle B+\phi)}.$ (Note, however, that $\sin (\angle B+\phi)=\sin (\angle C+\phi).)$ Further, let $Y$ be the foot of the perpendicular from $O$ to $QU.$ Then $\angle QOY=\angle BAO$ such that

$TU=OY=OQ\cdot\cos\angle QOY=OQ\cdot\sin (\angle B+\phi)=\frac{1}{2}BC.$

Denote $k=\sin (\angle B+\phi)$ and, as usual, $a=BC,$ $b=AC,$ $C=AB,$ and $p=\frac{1}{2}(a+b+c).$ Then, as we just saw, $\displaystyle AO=\frac{c}{2k},$ $\displaystyle AQ=\frac{b}{2k},$ and $\displaystyle OQ=\frac{a}{2k}.$ By the Pythagorean Theorem,

$\displaystyle\begin{align} TU^{2}&=OQ^{2}-QY^{2}\\ &=OQ^{2}-(QU-YU)^{2}\\ &=OQ^{2}-(AQ-AO)^{2}\\ &=\frac{1}{4k^2}(a-b+c)(a+b-c)\\ &=\frac{1}{k^2}(p-b)(p-c). \end{align}$

On the other hand, $\displaystyle k=\cos\frac{B-C}{2}$ and so $\displaystyle k^{2}=\frac{(b+c)^{2}(p-b)(p-c)}{a^{2}bc},$ implying

$\displaystyle TU^{2}=\frac{a^{2}bc}{(b+c)^{2}}.$

By the Law of Sines,

$\displaystyle\begin{align} a &= BC=BD+CD=\frac{c\sin\phi}{\sin (\angle ADB)}+\frac{c\sin\phi}{\sin (\angle ADC)}\\ &=(b+c)\frac{\sin\phi}{k}. \end{align}$

If $[S]$ denotes the area of shape $S$ then $\displaystyle [\Delta AOQ]=\frac{[\Delta ABC]}{(2k)^{2}}.$ If $X$ is the intersection of $AD$ and $OQ$ then $[\Delta AOQ]=\frac{1}{2}AX\cdot OQ$ from which

$\displaystyle AD=\frac{[\Delta ABC]}{OQk^{2}}=\frac{2[\Delta ABC]}{ak}=\frac{bc\sin(2\phi)}{ak}=\frac{2bc\sin (\phi)\cos (\phi)}{ak}.$

Thus, we may express $AD^{2}$ as

$\displaystyle AD^{2}=\frac{4bcp(p-a)}{(b+c)^{2}}.$

Finally, since $MN^{2}=AD^{2}+TU^{2},$ we get

$\displaystyle\begin{align} MN^{2} &=\frac{4bcp(p-a)}{(b+c)^{2}}+\frac{a^{2}bc}{(b+c)^{2}}\\ &=\frac{bc}{(b+c)^{2}}\left(4p(p-a)+a^{2}\right)\\ &=\frac{bc}{(b+c)^{2}}\left((b+c)^{2}-a^{2}+a^{2}\right)\\ &=bc, \end{align}$

ie., $MN^{2}=AB\cdot AC,$ as required.

71930994