Jordan Curve Theorem, Proof

JCT - Boundaries of the components of the complement of a Jordan curve II

Scott E. Brodie, MD, PhD
Icahn School of Medicine at Mount Sinai
New York

Recall: The boundary of each component of the complement is a subset of the Jordan curve.

In fact, the boundary of any component of the complement is the entire Jordan curve.

Suppose otherwise. Consider $x,$ $y$ in distinct components of a Jordan curve, respectively.

Recall: If a set does not separate $x,\;y,$ then no subset of it separates $x,\;y.$

Select a component of the complement of the Jordan curve which contains $x\;$ or $y.\;$
Since the boundary of a component is closed, if it omits a point of the Jordan curve, the inverse image of the boundary must therefore omit the corresponding point in the circle which is the pre-image of the Jordan curve.
But since the pre-image of the boundary is also closed, it must omit an open interval surrounding the omitted point.
But by the continuity of the inverse of the mapping which specifies the Jordan curve, the image of this open interval is an omitted open arc in the Jordan curve, and its complement, which contains the boundary, must be a (closed) Jordan arc.
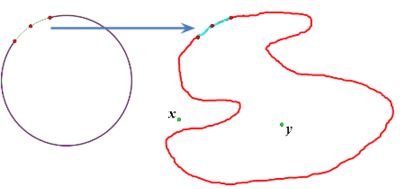
So ...
Since "boundaries separate," the boundary of the selected component separates $x,$ $y.$
But no Jordan arc separates the plane, so no subset of a Jordan arc, such as the boundary, can separate $x,$ $y.$
This contradiction implies that the boundary must be the entire Jordan curve.
Since the component was arbitrary, the (entire) Jordan curve must be the boundary of each component.

71534327