Jordan Curve Theorem, Proof
- JCT - Topology Toolbox
- JCT - Prologue
- JCT - Simple Cases
- JCT - Abstract Graphs and Eulerís Formula
- JCT - K3,3 and the Crossed Arcs Lemma
- JCT - Jordan Separation - the general case
- JCT - Boundaries of the components of the complement of a Jordan curve - I
- JCT - The Jordan Arc theorem
- JCT - Boundaries of the components of the complement of a Jordan curve II
- JCT - Uniqueness of the bounded component of the complement
- JCT - K3,3 on a Torus or Moebius Strip
- JCT - Sources
JCT - Boundaries of the components of the complement of a Jordan curve - I
Scott E. Brodie, MD, PhD
Icahn School of Medicine at Mount Sinai
New York
The boundary of a component of the complement of a Jordan curve is a subset of the Jordan curve:
The curve and the components of its complement partition the plane. As each component is open, it cannot contain any of its own boundary points, nor a boundary point of any other component. Thus the boundary must lie entirely within the Jordan curve.
a point of the boundary of an open set is accessible (from the open set) if it is the endpoint of an arc contained in the open set except for one endpoint (which is the boundary point itself).
Accessible points are dense in the boundary of an open set.
Proof
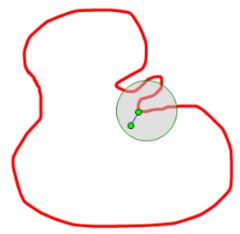
Given a point of the boundary, consider a closed disc centered on the boundary point, and choose a point of the disc in the interior of the open set. The intersection of the boundary with the closed disc is compact, so the distance from the chosen interior point to the boundary attains a minimum. The segment from the interior point to the boundary at which this minimum is attained lies within disc, and no point of the boundary comes between the interior and boundary points, which confirms that the endpoint on the boundary of this segment is accessible.
Note that this proposition implies that an open set is in a sense "co-extensive" with its boundary: not only is the boundary of an open set composed of points which are "close to" points of the set, but there are points of the open set close to all the points of its boundary.
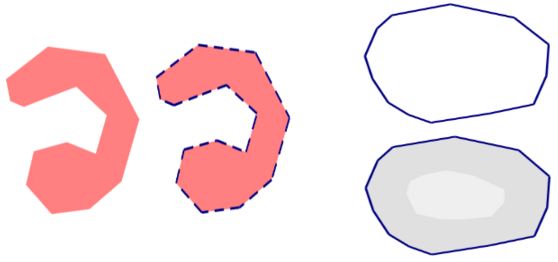
"Boundaries separate"
the boundary of an open set separates it from the complement of its closure.
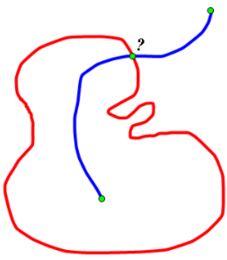
Draw an arc from a point of the set to a point in the interior of its complement. If this arc did not intersect the boundary, then the intersection of the original open set with the arc, and the intersection of the arc with the component of the complement containing the second point would constitute a disconnection of the arc; but any arc, as the image of a connected interval, is connected.
Jordan Curve Theorem, Proof
- JCT - Topology Toolbox
- JCT - Prologue
- JCT - Simple Cases
- JCT - Abstract Graphs and Eulerís Formula
- JCT - K3,3 and the Crossed Arcs Lemma
- JCT - Jordan Separation - the general case
- JCT - Boundaries of the components of the complement of a Jordan curve - I
- JCT - The Jordan Arc theorem
- JCT - Boundaries of the components of the complement of a Jordan curve II
- JCT - Uniqueness of the bounded component of the complement
- JCT - K3,3 on a Torus or Moebius Strip
- JCT - Sources
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
71542651
