Jordan Curve Theorem, Proof 

JCT - Jordan Separation, the general case

Scott E. Brodie, MD, PhD
Icahn School of Medicine at Mount Sinai
New York

  • The hypotheses for a Jordan curve are weak enough to admit many "pathological" curves:

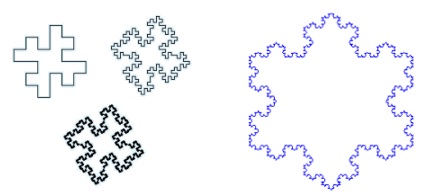
    • A Jordan curve need not be differentiable; indeed, it may even be nowhere-differentiable, such as many familiar "fractal" curves:

      Part5, fractal curves

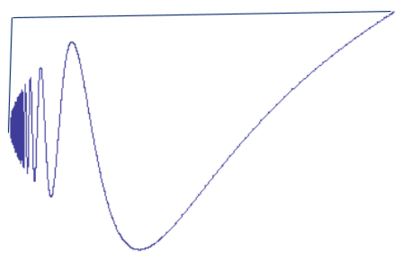
    • A Jordan curve need not be rectifiable – it may not have a well-defined finite length:

      Part5, not rectifiable curves

    • It can spiral:

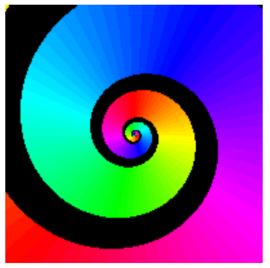
      Part5, spiral

    But useful features can still be noted:

    • Since a Jordan curve is the continuous image of a compact set, it is likewise compact, and therefore closed and bounded.

    • It can be enclosed in a circle or a rectangle

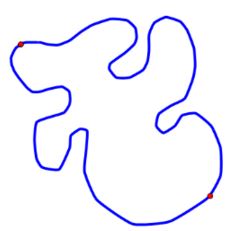
      Part5, curves and arcs

    • Any two distinct points on a Jordan curve mark off two Jordan arcs, which are disjoint except for their endpoints:

    • Thus a Jordan curve cannot fit inside a Jordan arc.

    • It has (one or more) topmost, bottom-most, left-most, and right-most points.

      Part5, extreme points

    • Select two points on a Jordan curve. Then the distance between the two points is a continuous function of the coordinates of the two points. As a continuous function on a compact set, it achieves a maximal value (perhaps more than once):

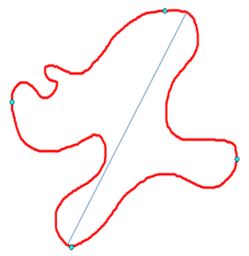
      Part5, two points

    • The set of intersections of Jordan curve with an arc or line segment may be infinite ...

    • But as the set of intersections is bounded, we can use the order of points on the line or arc to identify a least upper bound or greatest lower bound of the set of intersections.

    • Since the intersection of two closed sets is closed, these extrema are in fact themselves points of intersection. We can refer to them casually as the "first" or "last" such point.

    • As an aside, we can show that a Jordan curve (or arc) is "thin" – it cannot contain a disc:

    • Suppose otherwise. Then one can select a closed disc which is a proper subset of the curve. The circular boundary of this disc is a proper subset of the curve, whose inverse image is a closed proper subset of the original circle (or interval) mapped to the curve or arc, a Jordan curve in its own right.

      Part5, mapping

    • But the circle within the disc is a proper closed subset of the curve or arc, so its inverse image cannot be the entire circle or interval of the original domain. Indeed, the complement of any such closed proper subset must be open, and thus must contain an open subarc, so the inverse image can necessarily be contained in an arc which is a subset of the original domain. But such an arc cannot contain a Jordan curve!

      Part5, circles, circles

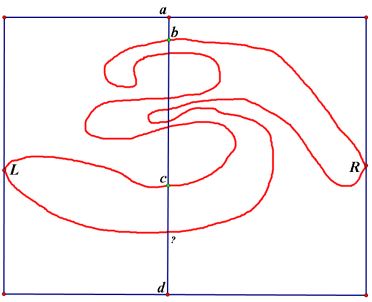
    • For example, enclose a Jordan curve in a rectangle, with leftmost and rightmost points $L\;$ and $R.\;$ These points separate the curve into upper and lower arcs. A segment $ad\;$ from the top of the rectangle to the bottom must intersect both arcs. Let $b,\;$ $c\;$ denote the first and last intersection with the upper arc. Then, by the Crossing Arcs Lemma, the compound arc $ab + bc + dc\;$ (where $bc\;$ is the portion of the upper arc cut off by $b\;$ and $c)\;$ must intersect the lower arc $LR,\;$ between $c\;$ and $d.\;$

      Part5, top to bottom

      The complement of a Jordan curve contains at least two components.

      Proof

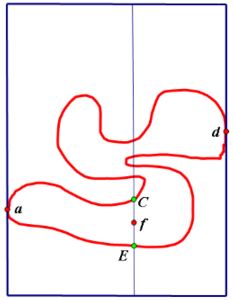
      Part5, labeled points

      • Orient the Jordan curve so that points of maximal separation lie on a horizontal line, and enclose the curve in a rectangle with horizontal and vertical sides which meets the curve only in its vertical sides, so that the entire curve falls within the interior of the rectangle, except for the points where it meets the vertical sides.

      • Label the uppermost intersections of the curve and the vertical sides as $a\;$ and $d.$

      • Draw another vertical line anywhere between the ve rtical sides of the rectangle.

      • By the Crossed Arcs Lemma, this line must intersect the upper and lower sub-arcs of the Jordan curve (which have endpoints on the vertical sides of the rectangle).

      • Going from top to bottom, note the last intersection of this intermediate line with the upper sub-arc, and the first intersection of the intermediate line with the lower sub-arc after the last intersection with the upper sub-arc. Label the last upper intersection and first lower intersection as $C\;$ and $E,\;$ respectively. Then segment $CE\;$ intersects the curve only at its endpoints.

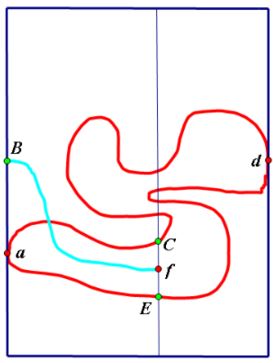
        Part5, separation

      • Draw an arc from an interior point, f, of CE to a point of the rectangle. We wish to show this arc must intersect the Jordan curve.

      • If it meets $a,$ $C,$ $d,$ or $E,\;$ we are done;

      • If not, label the first intersection of the arc with the rectangle as $B.$

      • If the arc $fB\;$ does not intersect the curve, then the points $a,$ $d,$ $f\;$ are all joined to the points $B,$ $C,$ $E\;$ by arcs or portions of the rectangle, and thus realize $K_{3,3}\;$ in the plane.

      • As this is impossible, we conclude that the arc $fB\;$ intersects the Jordan curve, and thus that the curve separates a (bounded) component of its complement, which contains the point $f,\;$ from the unbounded component of its complement.

    Jordan Curve Theorem, Proof 

    |Contact| |Front page| |Contents| |Geometry|

    Copyright © 1996-2018 Alexander Bogomolny

71536423