Jordan Curve Theorem, Proof
- JCT - Topology Toolbox
- JCT - Prologue
- JCT - Simple Cases
- JCT - Abstract Graphs and Eulerís Formula
- JCT - K3,3 and the Crossed Arcs Lemma
- JCT - Jordan Separation - the general case
- JCT - Boundaries of the components of the complement of a Jordan curve - I
- JCT - The Jordan Arc theorem
- JCT - Boundaries of the components of the complement of a Jordan curve II
- JCT - Uniqueness of the bounded component of the complement
- JCT - K3,3 on a Torus or Moebius Strip
- JCT - Sources
JCT - Prologue
Scott E. Brodie, MD, PhD
Icahn School of Medicine at Mount Sinai
New York
A circle has an inside and an outside...
The Jordan Curve Theorem (JCT) says that a simple closed curve (the continuous, 1-1 image of a circle) likewise separates the plane into an inside and an outside.
The proof has been elusive...

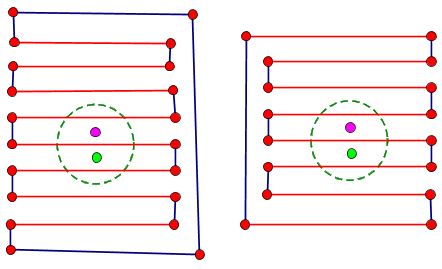
JCT is not "local",
It is impossible to tell which component is inside and which component is outside using only local information:
JCT holds only on certain 2-dimensional surfaces. For example, JCT fails on a torus or a Moebius strip:

We have little familiarity with "separation", and few tools which address it.
Much of our knowledge of well-behaved curves does not apply...
A Jordan curve need not be differentiable anywhere.
A Jordan curve need not be rectifiable.
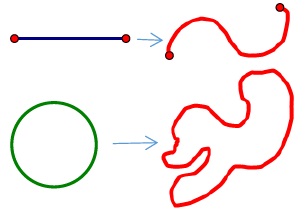
A Jordan curve is a homeomorphic image (image of a 1-1, continuous function with a continuous inverse) of a circle.
A Jordan arc is a homeomorphic image of a closed, bounded interval, such as $[0,1].$
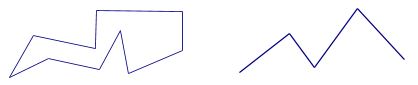
A (Jordan) polygon is a Jordan curve composed entirely of a finite number of straight line segments, which intersect only at their endpoints. A polygonal arc is a Jordan arc composed entirely of a finite number of straight line segments. We will adopt the convention that adjacent segments do not together form a larger segment. (In such a case, remove the intervening vertex, to obtain a larger segment.)
A set is disconnected if it can be partitioned into two non-empty subsets, both of which are open (in relative topology.) Equivalently, if it can be partitioned into two subsets, both of which are closed.

A set is connected if it is not disconnected. Equivalently, if its only subsets which are both open and closed (in relative topology) are the entire set and the empty set.
A set is path-connected if, for any two points in the set, there is a Jordan arc in the set whose endpoints are the two given points. A connected set need not be path-connected, but a set which is path-connected is always connected.

In the plane, an open, connected set is always path connected. Indeed, any two points of an open, connected set in the plane can be connected by a Jordan polygonal arc which lies entirely within the set.
A component of a set is a maximal connected subset.
The boundary of a set is its closure minus its interior; equivalently, it is the intersection of the set's closure with the closure of its complement.
Note the symmetry between the original set and its complement in this definition. It follows that the boundary of a set and the boundary of its complement coincide.
A subset separates a superset if the complement of the subset in the superset is disconnected. If x and y are points in the complement of a subset, then the subset separates the points x and y if they are elements of different components of the complement.
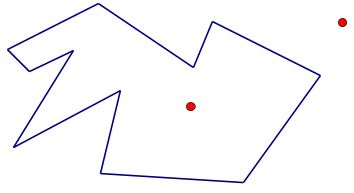
If a set separates $x$ and $y,$ then any superset which omits $x$ and $y$ also separates $x$ and $y,$ as the components containing $x$ and $y$ must remain disjoint:

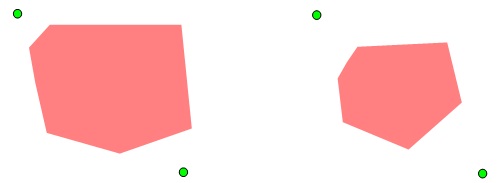
If a set omits $x$ and $y,$ and does not separate $x$ and $y,$ then no subset separates $x$ and $y,$ as enlarging the complementary component containing $x$ and $y$ cannot separate them.
- JCT - Topology Toolbox
- JCT - Prologue
- JCT - Simple Cases
- JCT - Abstract Graphs and Eulerís Formula
- JCT - K3,3 and the Crossed Arcs Lemma
- JCT - Jordan Separation - the general case
- JCT - Boundaries of the components of the complement of a Jordan curve - I
- JCT - The Jordan Arc theorem
- JCT - Boundaries of the components of the complement of a Jordan curve II
- JCT - Uniqueness of the bounded component of the complement
- JCT - K3,3 on a Torus or Moebius Strip
- JCT - Sources
Why is this so difficult?
Statement of the Jordan Curve Theorem (JCT):
In the plane, the complement of a Jordan curve consists of exactly two components, one bounded (the interior) and one unbounded (the exterior). Both the interior and exterior have the Jordan curve as their boundary.
In the course of proving JCT, we will also prove the Jordan Arc Theorem:
A Jordan arc does not separate the plane.
Definitions for JCT

Jordan Curve Theorem, Proof

|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
71532886
