Tiling a Chessboard with Dominoes

Even the simplest of all polyominoes - the domino - affords interesting puzzles. Here is one example [Levitin, #12]:

Is it possible to tile an 8×8 board with dominoes (2×1 tiles) so that no two dominoes form a 2×2 square.

Solution

References

1. S. Golomb, Polyominoes, Princeton University Press, 1994
2. A. Levitin and M. Levitin, Algorithmic Puzzles, Oxford University Press, 2011
3. G. E. Martin, Polyominoes, MAA, 1996
4. A. V. Shapovalov, The Principle of Narrow Places, MCCME, 2008 (free pdf, in Russian)

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

Is it possible to tile an 8×8 board with dominoes (2×1 tiles) so that no two dominoes form a 2×2 square.

Solution

The answer is, No, this is impossible, regardless of the board size. To see why, let's just start placing dominoes on the board one at a time and see where this leads us. Assuming, that it is possible to cover the board, a domino will have to be covering a corner square. Because of the symmetry, we may as well assume that the placement is as in the diagram below:

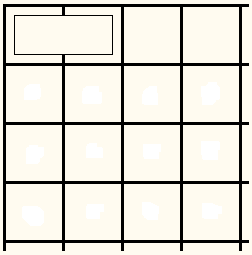
The question is where to place the second domino. If the covering is at all possible there have to be dominoes below the one that is already there. Placing it horizontally just below the first one creates a 2×2 square:

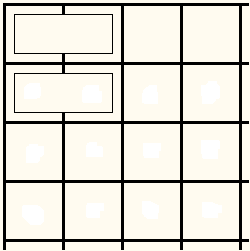
We are thus forced to place a square vertically:

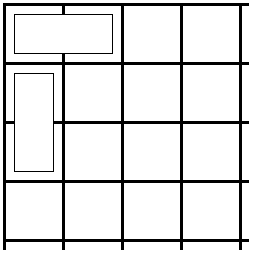
The two dominoes form a corner that needs to be filled. As before, a vertical domino will add up to a 2×2 square, so we are forced to place the third domino horizontally:

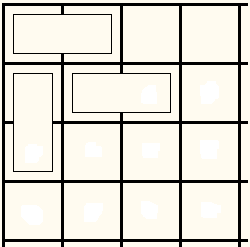
We get another corner to handle, and, again, a move is forced:

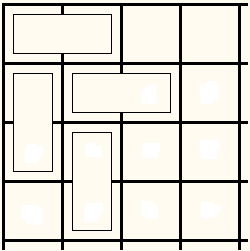
So we are forced to continue:

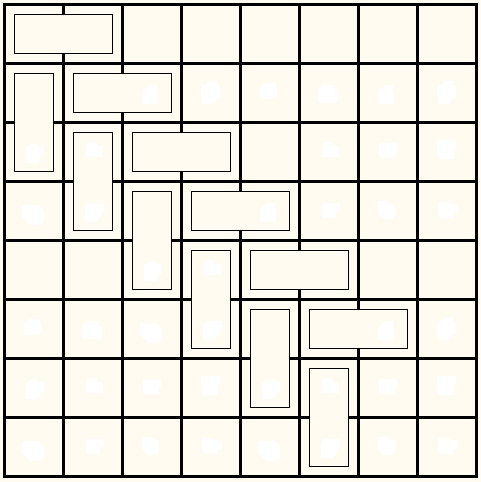
Now, reaching the bottom we see that the only way to continue is to create a 2×2 square which shows that the answer to the question at hand is negative. The same process actually shows that tiling of rectangles with one dimension odd and the other even is also impossible unless there is at least one 2×2 square.

Obviously this will happen with any square of even size, while there is no question about tiling an odd square.

Related material Read more...
	Covering A Chessboard With Domino
	Dominoes on a Chessboard
	Vertical and Horizontal Dominoes on a Chessboard
	Straight Tromino on a Chessboard
	Golomb's inductive proof of a tromino theorem
	Tromino Puzzle: Interactive Illustration of Golomb's Theorem
	Tromino as a Rep-tile
	Tiling Rectangles with L-Trominoes
	Squares and Straight Tetrominoes
	Covering a Chessboard with a Hole with L-Trominoes
	Tromino Puzzle: Deficient Squares
	Tiling a Square with Tetrominoes Fault-Free
	Tiling a Square with T-, L-, and a Square Tetrominoes
	Tiling a Rectangle with L-tetrominoes
	Tiling a 12x12 Square with Straight Trominoes
	Bicubal Domino

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny