Graphing Equations Is Useful, V
What Could This Be About?
Problem
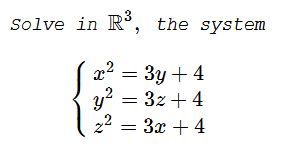
Solution 1
WLOG, $x\le y\le z\,$ such that $3x+4\le 3y+4\le 3z+4,\,$ implying $z^2\le x^2\le y^2,\,(*)$ from which, say, $z^2-x^2\le 0,\,$ i.e., $(z-x)(z+x)\le 0.\,$ But $z\ge x.\,$ Assume, for now, that $z\gt x.\,$ Then, $x+z\le 0.\,$ We'll consider two cases:
$\mathbf{x\lt z\le 0}$
$x\le y\le z\,\Longrightarrow\,x^2\ge y^2\ge z^2\,\Longrightarrow\,x^2\ge y^2.$
Comparing to (*), $x^2=y^2\,$ and, subsequently, $3y+4=3z+4,\,$ $x=y=z\,$ which contradicts $z\gt x.$
$\mathbf{x\le 0 \le z}\,\text{with }|x|\ge z$
Having $x\le y\le z\,$ suggests two cases: $x\le y\le 0\le z\,$ and $x\le 0\le y\le z.\,$ In the former case, $x^2\ge y^2\,$ which along with (*), would imply $x=y=z=0\,$ which is definitely not a solution. In the latter case, $|x|\ge z,\,$ so that again $x^2\ge y^2,\,$ with the same conclusion.
We may assume now that $z=x\,$ from which $z^2=x^2\,$ and, subsequently, $3x+4=3y+4\,$ such that $x=y\,$ and, therefore, $x=y=z.\,$ So what remains is to solve a quadratic equation $x^2=3x+4.\,$ With two roots, $-1\,$ and $4\,$ we have two solutions: $(x,y,z)=(-1,-1,-1)\,$ and $(x,y,z)=(4,4,4).$
Solution 2
We invert the first equation: $y=\displaystyle \frac{1}{3}(x^2-4)\,$ and consider iterations $x_{k+1}=f(x_k),\,$ with $f(x)=\displaystyle \frac{1}{3}(x^2-4).$
Relevant to the iterations are the points where the graph $y=f(x)\,$ intersects the diagonal, the so called the stationary (or fixed) points of function $f(x).\,$. These are the attractor $(-1,-1)\,$ and the repeller $(4,4).$ Iterations diverge if started with $x_0\gt 4\,$ or $x_0\lt -4.\,$ They converge to $(-1,-1)\,$ for $x_0\in (-4,4).$ There could be a danger that they settle into a finite loop around the attractor. The case of a $3\text{-loop}\,$ would solve our system. To see that there is no loop of any size, we'll prove that the distance to $x=-1\,$ decreases with iterations: $|x_{k+1}+1|\lt |x_k+1|.\,$ In other words, $\displaystyle \left|\frac{1}{3}(x^2-4)+1\right|\lt |x+1|.\;$ I.e., we wish to prove that, for $x\in (-4,4),$
$|x^2-1|\lt |3x+3|.$
Having to deal with absolute values, we'll consider four cases:
$\mathbf{x\ge 1}$
$3x+3\gt x^2-1\,\Longleftrightarrow\,-1\lt x\lt 4,\,$ well covering the range $4\gt x\gt 1.\,$ The required inequality verifies in this case.
$\mathbf{|x|\lt 1}$
$3x+3\gt 1-x^2\,\Longleftrightarrow\,-1\gt x\,\text{or}\,x\lt -2,\,$ well covering the range $|x|\lt 1.\,$ The required inequality verifies in this case.
$\mathbf{-2\le x\lt -1}$
$-3x-3\gt x^2-1\,\Longleftrightarrow\,-2\le x\le -1,\,$ just as needed. The required inequality verifies in this case.
$\mathbf{-4\lt x\le -2}$
In the case, the inequality $-3x-3\gt x^2-1\,$ does not hold, as we just saw. This is because starting in $(-4,-2)\,$ the iterations jump over the $y\text{-axis},\,$ away from $x=-1.\,$ However, in this case, the iterations fall into the interval $(0,4)\,$ from which they continue to converge (according to the previous three cases) to $x=-1.\,$ To see that, let
$-4\lt x\lt -2\,\Longleftrightarrow\, 16\gt x^2\gt 4\,\Longleftrightarrow\,4\gt\displaystyle\frac{1}{3}(x^2-4)\gt 0,$
which completes the proof. The only solutions a finite sequence of iterations may have are defined by the stationary points. In case of three equations, there are two solutions $(x,y,z)=(-1,-1,-1)\,$ and $(x,y,z)=(4,4,4).\,$ Note that the logic does not discriminate between the number of equations. E.g., the system
$\begin{cases} u^2=3v+4&\\ v^2=3w+4&\\ w^2=3x+4&\\ x^2=3y+4&\\ y^2=3z+4&\\ z^2=3u+4& \end{cases}$
has two solutions $(-1,-1,-1,-1,-1,-1)\,$ and $(4,4,4,4,4,4).$
Solution 3 (Illustrated)
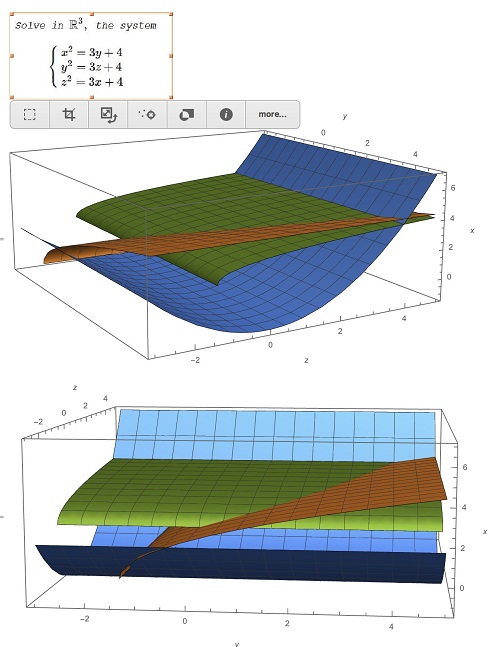
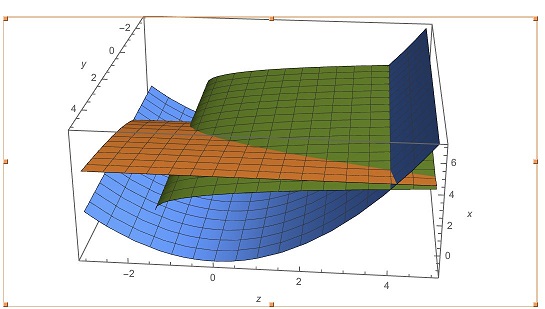
Clearer.
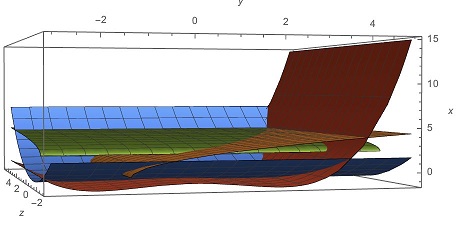
Solution 4
Noting that a homogeneous set of equations has a trivial solution $(0,0,0),\,$ let us homogenize the equations. Let $x=p+k,\,$ $y=q+k,\,$ and $z=r+k.\,$ Thus, $x^2=3y+4$ implies $p^2+2pk+k^2=3q+3k+4.\,$ Let $k^2=3k+4\,$ to get rid of the constant terms. There are two solutions $k=-1\,$ and $k=4.\,$
Choose $k=-1.\,$ Thus, $x=p-1,\,$ $y=q-1,\,$ and $z=r-1.\,$ The homogeneous equations become $p^2=2p+3q,\,$ $q^2=2q+3r,\,$ and $r^2=2r+3p.\,$ The trivial solution of $(p=0,q=0,r=0)\,$ gives $(x=-1,y=-1,z=-1).\,$
Alternatively, if we choose $k=4\,$ we get, $x=p+4,\,$ $y=q+4,\,$ and $z=r+4.\,$ The equations become $p^2=-8p+3q,\,$ $q^2=-8q+3r,\,$ and $r^2=-8r+3p.\,$ The trivial solution gives $(x=4,y=4,z=4).\,$
We now need to see if there are any other solutions. To do this, we let $l=x-3/2,\,$ $m=y-3/2,\,$ $n=z-3/2$ $(3/2\,$ is the midpoint of the two solutions already found). The equations become $l^2=-3(l-m)+25/4,\,$ $m^2=-3(m-n)+25/4,\,$ $n^2=-3(n-l)+25/4.\,$ Without loss in generality, let $l\ge mge n.\,$ Thus, the first equation gives $l^2\le 25/4.\,$ The third equation gives $n^2\ge 25/4.\,$ Thus, $l^2\ge 25/4$ as $l\ge n.\,$ This is only possible if $l^2=25/4\,$ and $n^2=25/4.\,$ Adding the three equations, $l^2+m^2+n^2=75/4.\,$ Thus, $m^2=25/4.\,$ Replacing the square terms in the equations with $25/4,\,$ we see that $l=m=n.\,$ The only solutions that satisfy these conditions are the two solutions that we have found.
Acknowledgment
I've lifted this problem from the Imad Zak facebook group. Solution 1 by Imad Zak. The problem fits into a general framework as emerges in Solution 2; Solution 3 is by N. N. Taleb; Solution 4 is by Amit Itagi.
Systems of Iterated Equations
- Iterations on Monotone Functions
- Graphing Equations Is Useful
- Graphing Equations Is Useful, II
- Graphing Equations Is Useful, III
- Graphing Equations Is Useful, IV
- Graphing Equations Is Useful, V
- Tangential Chaos
- Equation in Radicals as a System of Equations
- Two Conditions for a Triangle to Be Equilateral
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny71534716
