Double and Half Angle Formulas

Three formulas are usually referred to as "double angle formulas":

$\begin{align} \sin 2\alpha &= 2\sin\alpha \cdot\cos \alpha ,\\ \cos 2\alpha &= \cos^{2}\alpha - \sin^{2}\alpha ,\\ \cos 2\alpha &= 2\cos^{2}\alpha - 1 ,\\ \cos 2\alpha &= 1 - 2\sin^{2}\alpha ,\\ \displaystyle\tan 2\alpha &= \frac{2\tan\alpha}{1-\tan^{2}\alpha}. \end{align}$

The first two formulas are a specialization of the corresponding addition formulas; the third and the fourth follow directly from the second with an application of the Pythagorean identity, $\cos^{2}\alpha + \sin^{2}\alpha = 1.$ The fourth follows from the first two and the definition of tangent.

They can also be observed in a proof without words illustrated by the following diagram that depicts a semicircle and several associated right triangles [Nelsen]:

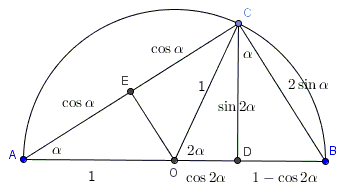
Double angle formula PWW

For example, the area of $\Delta ABC$ can be computed in two ways so that $AC\cdot BC=AB\cdot CD$ which is the first formula. Further, since triangles $ACD$ and $ABC$ are similar, $\displaystyle\frac{AD}{AC}=\frac{AC}{AB},$ i.e.,

$\displaystyle\frac{1+\cos 2\alpha}{2\cos\alpha}=\frac{2\cos\alpha}{2},$

which is the third formula, $\cos 2\alpha = 2\cos^{2}\alpha - 1.$

From $\Delta BCD,$ $\displaystyle\tan\alpha=\frac{1-\cos 2\alpha}{\sin 2\alpha},$ and from $\Delta ACD,$ $\displaystyle\tan\alpha=\frac{\sin 2\alpha}{1+\cos 2\alpha},$ both of which are known under the moniker of "half-angle formulas" because they could be rewritten as

$\displaystyle\tan\frac{\beta}{2}=\frac{1-\cos \beta}{\sin\beta}$

and

$\displaystyle\tan\frac{\beta}{2}=\frac{\sin\beta}{1+\cos\beta}.$

Other half-angle formulas are derived from the above. For example,

$\displaystyle\cos\frac{\beta}{2}=\pm\sqrt{\frac{1+\cos \beta}{2}}$

and

$\displaystyle\sin\frac{\beta}{2}=\pm\sqrt{\frac{1-\cos \beta}{2}}.$

The latter formulas lead to other that I am sure many would find exciting if not beautiful.

Taking $\displaystyle\beta=\frac{\pi}{2},$ and recollecting that $\displaystyle\cos\frac{\pi}{2}=0,$ the first of these gives (since cosine is positive in the first quadrant)

$\displaystyle\cos\frac{\pi}{4}=\sqrt{\frac{1}{2}}=\frac{\sqrt{2}}{2},$

which just verifies a value of $\displaystyle\cos\frac{\pi}{4}.$ But the idea is to continue: let now $\displaystyle\beta=\frac{\alpha}{4}:$

$\displaystyle\cos\frac{\pi}{8}=\sqrt{ \frac{1+\cos\frac{\pi}{4}}{2} }=\frac{1}{2}\sqrt{2+\sqrt{2}}.$

The next term in the sequence is

$\displaystyle\cos\frac{\pi}{16}=\frac{1}{2}\sqrt{2+\sqrt{2+\sqrt{2}}}$

and the one after

$\displaystyle\cos\frac{\pi}{32}=\frac{1}{2}\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}.$

The general expression can be guessed (and if need be proved by induction):

$\displaystyle\cos\frac{\pi}{2^n}=\frac{1}{2}\underbrace{\sqrt{2+\sqrt{2+\sqrt{2+\ldots+\sqrt{2}}}}}_{n-1\space\mbox{radicals}}.$

Since cosine is a continuous function and $\displaystyle\lim_{n\rightarrow\infty}\frac{\pi}{2^n}=0,$

$\displaystyle\lim_{n\rightarrow\infty}\frac{1}{2}\underbrace{\sqrt{2+\sqrt{2+\sqrt{2+\ldots+\sqrt{2}}}}}_{n\space\mbox{radicals}}=1.$

In a similar manner we can obtain

$\displaystyle\sin\frac{\pi}{2^n}=\frac{1}{2}\underbrace{\sqrt{2-\sqrt{2+\sqrt{2+\ldots+\sqrt{2}}}}}_{n-1\space\mbox{radicals}}.$

But the limit it leads to is rather unexpected. It's a well known result that $\displaystyle\lim_{x\rightarrow 0}\frac{\sin x}{x}=1,$ from which

$\displaystyle\lim_{n\rightarrow\infty}\frac{ \sin\frac{\pi}{2^n} }{\frac{\pi}{2^n}}=1,$

and, as a combination of the latest two equalities,

$\displaystyle\pi=\lim_{n\rightarrow\infty}2^{n}\underbrace{\sqrt{2-\sqrt{2+\sqrt{2+\ldots+\sqrt{2}}}}}_{n\space\mbox{radicals}}.$

The double-angle formula for sine also leads to an engaging limit, first discovered by L. Euler. Note that

$\begin{align} \sin x &= 2\sin\frac{x}{2}\cos\frac{x}{2}\\ &= 2^2\sin\frac{x}{4}\cos\frac{x}{4}\cos\frac{x}{2}\\ &= 2^3\sin\frac{x}{8}\cos\frac{x}{8}\cos\frac{x}{4}\cos\frac{x}{2}\\ &= 2^4\sin\frac{x}{16}\cos\frac{x}{16}\cos\frac{x}{8}\cos\frac{x}{4}\cos\frac{x}{2}\\ &\cdots\\ &= 2^n\sin\frac{x}{2^n}\cos\frac{x}{2^n}\ldots\cos\frac{x}{8}\cos\frac{x}{4}\cos\frac{x}{2}\\ &\cdots \end{align}$

Multiply and divide by $x$ to obtain a little different form:

$\sin x=x\displaystyle\frac{\sin\frac{x}{2^n}}{\frac{x}{2^n}}\prod_{k=1}^{n}\cos\frac{x}{2^k},$

which, with $\displaystyle x=\frac{\pi}{2},$ gives

$1=\displaystyle\frac{\pi}{2}\frac{\sin\frac{\pi}{2^{n+1}}}{\frac{\pi}{2^{n+1}}}\prod_{k=1}^{n}\cos\frac{\pi}{2^{k+1}},$

and, going to the limit:

$\displaystyle\frac{2}{\pi}=\lim_{n\rightarrow\infty}\prod_{k=1}^{n}\cos\frac{\pi}{2^{k+1}}.$

Taking into account the radical expressions for $\displaystyle\cos\frac{\pi}{2^k}$ derived earlier, we arrive at Euler's formula [Maor]:

$\displaystyle\frac{2}{\pi}=\frac{\sqrt{2}}{2} \frac{\sqrt{2+\sqrt{2}}}{2} \frac{\sqrt{2+\sqrt{2+\sqrt{2}}}}{2} \frac{\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}}{2}\ldots$

References

I. M. Gelfand, M. Saul, Trigonometry, Birkhäuser, 2001 (145-152, 163-167)
E. Maor, Trigonometric Delights, Princeton University Press, 1998 (90, 140, 146,161)
R. B. Nelsen, Proofs Without Words, MAA, 1993 (34-35)

Trigonometry

71947077