An Inequality with Constraint XIX

Statement

an inequality with constraints, #19

Solution 1

Recollect that

  1. $9(x+y+(y+z)(z+x)\ge 8(x+y+z)(xy+yz+zx),$
  2. $(xy+yz+zx)^2\ge xyz(x+y+z).$

    3. Using these and the given condition, $x+y+z=1,$ we obtain

    $\displaystyle\begin{align} (x+y)(y+z)(z+x)&\ge\frac{8}{9}(x+y+z)(xy+yz+zx)\\ &=\frac{8}{9}(xy+yz+zx)\\ &\ge\frac{8}{9}\sqrt[3]{3xyz(x+y+z)}\\ &=\frac{8}{3\sqrt{3}}\sqrt{xyz}. \end{align}$

    This gives us

    $\displaystyle\frac{\sqrt{xyz}}{(x+y)(y+z)(z+x)}\le\frac{3\sqrt{3}}{8},$

    as required.

Solution 2

An incarnation of Mitrinovic's formula:

Setting $a=y+z,\,$ $b=z+x,\,$ $c=x+y,\,$ $a,b,c$ are the side lengths of $\Delta ABC.\,$ The semiperimeter $s=x+y+z=1;\,$ the area $S=\sqrt{xyz(x+y+z)}=\sqrt{xyz};\,$ the circumradius $\displaystyle R=\frac{abc}{4S}=\frac{(x+y)(y+z)(z+x)}{4\sqrt{xyz}}.\,$ We, thus, have

$\displaystyle\begin{align} &s\le\frac{3\sqrt{3}R}{2}\,&\Leftrightarrow\\ &1\le\frac{3\sqrt{3}}{2}\cdot\frac{(x+y)(y+z)(z+x)}{4\sqrt{xyz}}\,&\Leftrightarrow\\ &\frac{\sqrt{xyz}}{(x+y)(y+z)(z+x)}\le\frac{3\sqrt{3}}{8}. \end{align}$

Solution 3

$\displaystyle\begin{align} &\sqrt{xyz(x+y+z)}\le\sqrt{3}(xy+yz+zx)\,&\Rightarrow\\ &(x+y+z)\sqrt{xyz(x+y+z)}\le\sqrt{3}(xy+yz+zx)(x+y+z). \end{align}$

But

$\displaystyle\frac{\sqrt{3}(xy+yz+zx)(x+y+z)}{9}\le\frac{\sqrt{3}(x+y)(y+z)(z+x)}{8}.$

Solution 4

Using Lagrange's multipliers<

an inequality solved with Lagrange's multipliers

Note that the left-hand side is concave and attains its maximum of $\displaystyle\frac{3\sqrt{3}}{8}:$

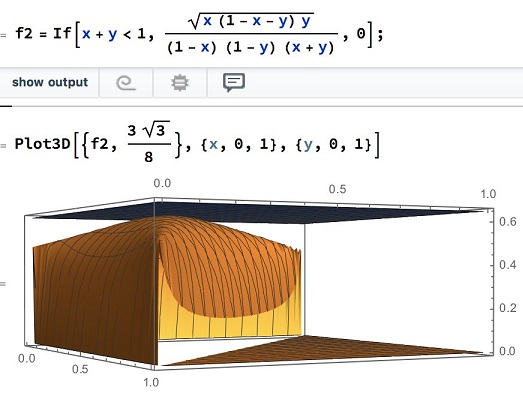
an inequality with concave function

Solution 5

Let's set $x+y=a,$ $y+z=b,$ $x+z=c.$ Then $a,b,c$ are sides of a triangle. By Heron's formula,

$\displaystyle LHS = Area(triangle)/abc = 1/(4R),$

where $R$ is the circumradius of the triangle. It's well known that circumradius is minimum if triangle is equilateral. Simple calculation (see below) leads to $\displaystyle max \frac{1}{4R}= 3\sqrt(3)/8.$

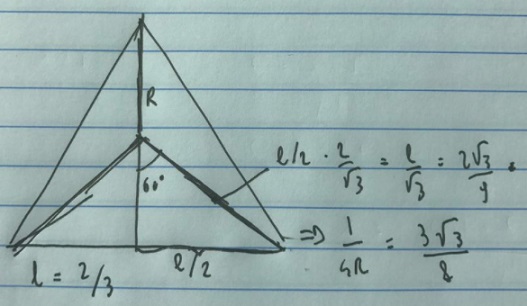
circumradius is minimum in equilateral triangle

The fact that xyz is actually the area of the triangle looked like some kind of miracle :D

Solution 6

Due to the constraints, one of the variables is not less than $\displaystyle\frac{1}{3}.\,$ WLOG, assume that's $\displaystyle x\ge\frac{1}{3}.\,$ Then $z=1-x-y\,$ and look at

$\displaystyle f(y)=\frac{\sqrt{xy(1-x-y)}}{(x+y)(1-x)(1-y)},$

with $0\le y\le 1-x.\,$ Further,

$\displaystyle f'(y)=\frac{\sqrt{x}}{1-x}\cdot\frac{(1-x-2y)(y^2+(x-1)y+x)}{2(x+y)^2(1-y)^2\sqrt{y-xy-y^2}}$

which vanishes only when $\displaystyle y=\frac{1-x}{2}\,$ since $y^2+(x-1)y+x\,$ is never $0\,$ because $\displaystyle x\ge\frac{1}{3}!$

Thus maximum happens when $\displaystyle y=\frac{1-x}{2},\,$ i.e.,

$\displaystyle f_{max}(y)=\frac{\displaystyle\sqrt{x\left(\frac{1-x}{2}\right)\left(\frac{1-x}{2}\right)}}{\displaystyle\left(\frac{1+x}{2}\right)(1-x)\left(\frac{1+x}{2}\right)}=\frac{2\sqrt{x}}{(1+x)^2},$

where $\displaystyle\frac{1}{3}\le x\le 1.$ The right-hand side is decreasing on $\displaystyle \left[\frac{1}{3},1\right),\,$ so its maximum is attained at $\displaystyle x=\frac{1}{3}:$

$\displaystyle \frac{2\sqrt{x}}{(1+x)^2}\bigg|_{x=\frac{1}{3}}=\frac{\displaystyle2\sqrt{\frac{1}{3}}}{\displaystyle\left(\frac{4}{3}\right)^2}=\frac{3\sqrt{3}}{8}.$

Acknowledgment

The problem, with a solution (Solution 1) by Hung Nguyen Vet, was kindly posted at the CutTheKnotMath facebook page by Dan Sitaru. He later added a solution of his own (Solution 2). Solution 3 is by Leo Giugiuc; Solution 4 is by N. N. Taleb; Proof 5 is by Lorenzo Villa; Solution 6 is by Sam Walters. Dan has previously published the problem at the Romanian Mathematical Magazine.

 

Inequalities with the Sum of Variables as a Constraint

|Contact| |Front page| |Contents| |Algebra|

Copyright © 1996-2018 Alexander Bogomolny

71537512