Probability in Dart Throwing
Problem

Solution 1
The region where points are closer to the center of the square than to an edge, is the intersection of the interiors of four parabolas:
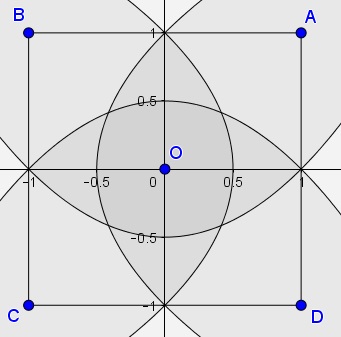
The probability sought is the ratio of the area of that region to the area of the square whose side was chosen to be $2.$
The region can be seen to consist of $8$ congruent pieces:
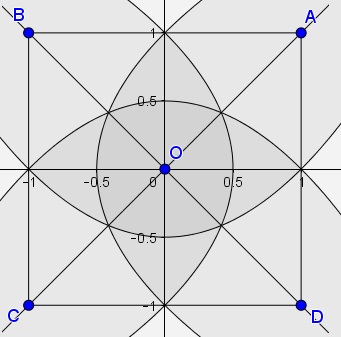
Thus, suffice it to calculate the area of one of them. Note also that the square also consists of $8$ parts each housing one part of the region. So, we need only compare the areas of these two.
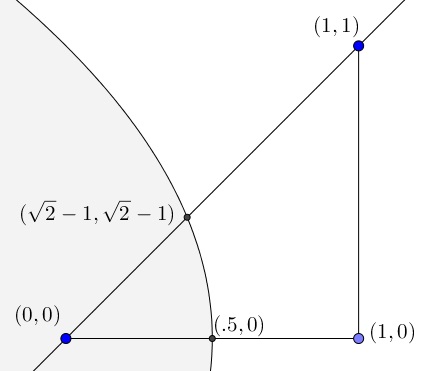
The parabola is defined by the equation $1-x=\sqrt{x^2+y^2},$ or $\displaystyle x=\frac{1-y^2}{2}.$ Its intersection with the diagonal $y=x$ is found from $x^2+2x-1=0$ to be $(\sqrt{2}-1,\sqrt{2}-1).$
It is easier to integrate by $y$ than by $x.$ The area of the shaded region within the triangle is
$\displaystyle \begin{align} \int_0^{\sqrt{2}-1}\left(\frac{1-y^2}{2}-y\right)dy&=\left[\frac{y}{2}-\frac{y^2}{2}-\frac{y^3}{6}\right]^{\sqrt{2}-1}_0\\ &=\frac{\sqrt{2}-1}{2}-\frac{(\sqrt{2}-1)^2}{2}-\frac{(\sqrt{2}-1)^3}{6}\\ &=\frac{4\sqrt{2}-5}{6}. \end{align}$
The area of the triangle is $\displaystyle \frac{1}{2}\cdot 1\cdot 1=\frac{1}{2}$ and the ratio of the two $\displaystyle \frac{4\sqrt{2}-5}{3}.$
Solution 2
Using symmetry, the problem can be analyzed in the first octant. Let the side of square be $2$. The curve that divides the region into points closer to either the vertex of the vertical edge is the parabola with focus at the vertex and directrix as the vertical edge.
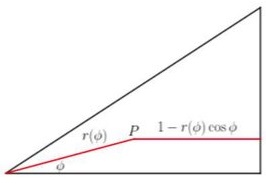
Let a point $P$ in the octant have polar coordinates $(r,\phi)$. Its distance from the vertex is $r$ and that from the edge is $r(1-\cos\phi)$. Thus, the equation of the parabola is
$\displaystyle r(\phi)=\frac{1}{1+\cos \phi}.$
Hence, the required probability is
$\displaystyle \begin{align} P&=\frac{\text{Area on the vertex side of the parabola}}{\text{Area of the triangle}}=2\int_{0}^{\pi/4} \frac{1}{2}r^2(\phi) d\phi \\ &=\int_{0}^{\pi/4} \frac{d\phi}{(1+\cos\phi)^2} =\left.\frac{\sin \phi (2+\cos\phi )}{3(1+\cos\phi)^2}\right\vert_{0}^{\pi/4} =\frac{\left(4\sqrt{2}-5\right)}{3}\sim 0.219. \end{align}$
Solution 3
We generalize the question to $n-gons.$ The region of points that are closer to the center than to the boundary of the $n-gon$ is the intersection of the interiors of $n$ parabolas, with a $2n-fold$ symmetry. Thus we need only to focus on one of $2n$ wedges.
Let the center of a regular $n-gon$ be at the origin. Take an edge being the line $x=1$. Mixing in polar coordinates, cut the line off at $\theta =0$ and at $\displaystyle \theta = \frac{\pi}{n}$. The boundary of the bullseye/target where the center is nearer than the edge is given by a parabolic arc with focus at $0$ and directrix at $x=1$. The equation for this is $\displaystyle r=\frac{1}{1+cos(\theta)}$. We only look at the right triangular wedge between $\theta=0$ and $\displaystyle \theta=\frac{\pi}{n}$ and then exploit symmetry.
We want the probability of being closer to the origin than this boundary, so we use polar integration:
$\displaystyle \begin{align} \frac{1}{2}\int_{0}^{\frac{\pi}{n}}\left(\frac{1}{1+\cos\theta}\right)^2d\theta &= \frac{1}{8}\int_0^{\frac{\pi}{n}}\sec^4\frac{\theta}{2}d\theta\\ &= \frac{1}{16}\left(\frac{4}{3}\tan^3\left(\frac{\pi}{2n}\right)+4\tan\left(\frac{\pi}{2n}\right)\right)\\ &=\frac{1}{12}\cdot\tan\left(\frac{\pi}{2n}\right)\left(\sec^2\left(\frac{\pi}{2n}\right)+2\right)\\ &=\frac{1}{12}\left(\frac{\sin(\frac{\pi}{n})}{1+\cos(\frac{\pi}{n})}\right)\left(\frac{2}{1+\cos(\frac{\pi}{n})}+2\right)\\ &={1}{6}\sin\left(\frac{\pi}{n}\right)\left(\frac{2+\cos(\frac{\pi}{n})}{(1+\cos(\frac{\pi}{n}))^2}\right). \end{align}$
Since the area of the triangle is $\tan({\pi\over n})/2$ we have a probability of
$\displaystyle \begin{align} &{1\over 3}\cos({\pi\over n})\left(2+\cos({\pi\over n})\over (1+\cos({\pi\over n}))^2\right)={1\over 3}\left((1+2\cos({\pi\over n})+\cos^2({\pi\over n})-1)\over (1+\cos({\pi\over n}))^2\right)\\ &={1\over 3}\left(1-{1\over (1+\cos({\pi\over n}))^2}\right). \end{align}$
Remark 1
From the last formula,
$\displaystyle \lim_{n\to\infty}{1\over 3}\left(1-{1\over (1+\cos({\pi\over n}))^2}\right)=\frac{1}{3}\cdot\frac{1}{4}={1\over 4}.$
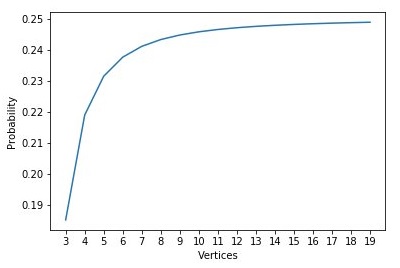
Interestingly, this limit could be found with additional calculations. As $n$ grows, $n-gon$ approaches a circle and, due to symmetry, the same happens with the intersection of the parabolas. The radius of the former is twice the radius of the latter and their areas are in the ratio $4:1.$
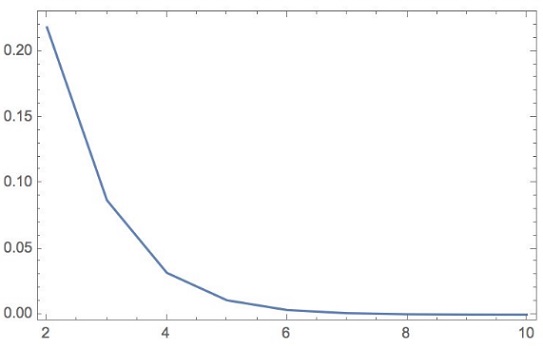
Remark 2
An analogous problem formulated in higher dimensions leads to a surprising result: the probability of getting nearer to center than to the edge tends to zero:
Acknowledgment
This is problem 1999-5 from the A Friendly Mathematics Competition by Rick Gillman (ed.)
Solution 2 and Remark 1 are by Amit Itagi (the graph there is by Adisetyo P.) Solution 3 is by Derek Boeckner.
Remark 2 follows the tweets of N. N. Taleb (more authentically: "This is the curse of dimensionality behind $P\ne NP$ we used with GMO idiots"), the calculations and the graph are by Marcos Carreira.
|Contact| |Front page| |Contents| |Probability|
Copyright © 1996-2018 Alexander Bogomolny71534716
