Probability of First Digit in Product
Problem

Solution 1
We shall represent integers with $d$ digits as $N=m\cdot 10^{d-1},$ with $1\le m\lt 10.$ Then for two integers, $N_1=m_1\cdot 10^{d-1}$ and $N_2=m_2\cdot 10^{d-1},$ $N_1N_2=m_1m_2\cdot 10^{2d-2},$ with $1\le m_1m_2\lt 100.$ The first digit of the product is $n,$ provided $m_1m_2\in \left[n,n+1\right)\bigcup \left[10n,10(n+1)\right).$
The totality of the products $m_1m_2$ fills proportionally the bands defined by the hyperbolas $xy=n$ and $xy=10n$ in the interior of the square $(1,1)-(10,10).$ Thus the sought limit probabilities (that I'll denote $P^n)$ are the areas of those bands relative to the area of the square, which is $81:$
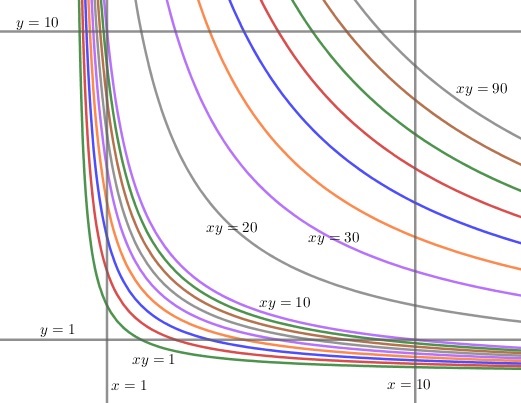
For $n=9,$ the calculations differ somewhat from the rest of the digits:
$\displaystyle \begin{align} 81P^9&=\left[\int_1^9\left(\frac{10}{x}-\frac{9}{x}\right)dx+\int_9^{10}\left(\frac{10}{x}-1\right)dx\right]+\int_9^{10}\left(10-\frac{90}{x}\right)dx\\ &=\int_1^9\frac{1}{x}dx+\int_9^{10}\left[\left(\frac{10}{x}-1\right)+\left(10-\frac{90}{x}\right)\right]dx\\ &=\ln x\big|_1^9+\left(9x-80\ln x\right)\big|_9^{10}\\ &=9+81\ln 9-80\ln 10. \end{align}$
For $n\ne 9,$ we'll run the calculations piecemeal:
$\displaystyle\begin{align}[\text{Area below }xy=10n]=U(n)&=9n+\int_n^{10}\frac{10n}{x}dx\\ &=9n+10n\ln x\big|_n^{10}=9n+10n\ln\frac{10}{n}. \end{align}$
$\displaystyle\begin{align}[\text{Area below }xy=n]=L(n)&=\int_1^n\frac{n}{x}dx\\ &=n\ln x\big|_1^{n}=n\ln n. \end{align}$
Then
$\displaystyle \begin{align} P^n&=\left[U(n+1)-U(n)\right]+\left[L(n+1)-L(n)\right]\\ &=9n\ln n-(n+1)\ln (n+1)+9+10\ln 10. \end{align}$
Solution 2
If the $d-digit$ number is written in scientific notation, the significand is uniformly distributed between $1$ and $10$ (as $d\rightarrow\infty$). For illustrative purposes, $2936$ is $2.936\times 10^3$ in scientific notation; $2.936$ is the significand.
The mantissa of the $\log_{10}$ of the number or the $\log_{10}$ of the significand has a probability density function of $f(x)=C\cdot 10^x$ over $x\in[0,1)$, where $C$ is a normalization constant - $1/\int_{0}^1 10^x dx$ - that turns out to be $\ln(10)/9$. If $m_1$ and $m_2$ are the mantissas for the two numbers being multiplied, the mantissa of the product is $M=(m_1+m_2)-\lfloor m_1+m_2\rfloor.$ If $M\in[\log_{10}D,\log_{10}(D+1))$, then the first digit of the product is $D$.
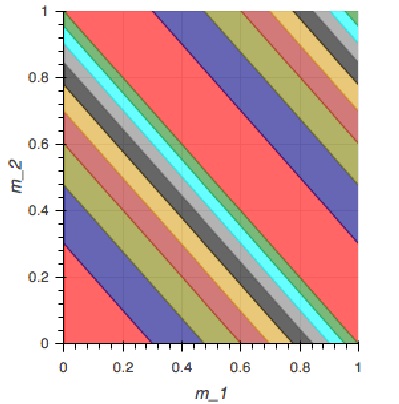
The figure shows the joint space of $m_1$ and $m_2$. The partitions of the shaded regions are at $m_1+m_2$ values of $\log_{10}{2}-\log_{10}{10}$ and $(1+\log_{10}{2})-(1+\log_{10}{19})$. The partitioned regions come in pairs where regions with the same color have the same value of $M$ and thus the same first digit $D$. The red region has first digit $1$, the blue $2$ and so on until the last green region has first digit $9$. Thus, the probability of having digit $D$ as the first digit is
$\displaystyle\begin{align} P(D)&=\bigg\{ \int_{m_2=0}^{\log_{10}{(D+1)}}\int_{m_1=0}^{\log_{10}(D+1)-m_2}-\int_{m_2=0}^{\log_{10}{D}}\int_{m_1=0}^{\log_{10}(D)-m_2}\\ &+\int_{m_2=\log_{10}D}^{1}\int_{m_1=1+\log_{10}D-m_2}^1 \\ &-\int_{m_2=\log_{10}(D+1)}^{1}\int_{m_1=1+\log_{10}(D+1)-m_2}^1\bigg\}f(m_1)f(m_2)dm_1dm_2 \\ &=\frac{1}{81}\left[(D+1)\ln(D+1)-D\ln(D)-1\right] \\ &+\frac{10}{81}\left[D\ln(D)-(D+1)\ln(D+1)+1+\ln(10)\right] \\ &=\frac{1}{9}\left[D\ln(D)-(D+1)\ln(D+1)+1\right]+\frac{10\ln(10)}{81}. \end{align}$
The computed values are shown in the table:
$\begin{array}{r|rr} \text{Leading digit}&&\text{Probability}\\ \hline 1&& 0.241348\\ 2&& 0.183209\\ 3&& 0.145454\\ 4&& 0.117380\\ 5&& 0.095007\\ 6&& 0.076402\\ 7&& 0.060474\\ 8&& 0.046549\\ 9&& 0.034178 \end{array}$
Solution 3
$x,y \approx \text{UniformDistribution}[\{L,H\}]$ and independent. The product has (long story) for PDF $\varphi(.)$
$\varphi(z)=\begin{array}{cc} \Bigg\{ & \begin{array}{cc} \frac{\log \left(\frac{H^2}{z}\right)}{(H-L)^2} & H^2>z\land H L\lt z \\ \frac{\log \left(\frac{z}{L^2}\right)}{(H-L)^2} & H L\geq z \\ \end{array} \\ \end{array}$
We have
$\displaystyle \int_{L^2}^{H^2} \varphi(z) =1 \; \text{ (verification for paranoid people)}$
$\displaystyle \begin{align} P_1&=\int_{9 L^2}^{10 L^2} \varphi(z) \, dz=-\frac{L^2 (1+9 \log (9)-10 \log (10))}{(H-L)^2}\\ P_2&=\int_{\frac{9}{10}(H+1)^2}^{H^2} \varphi(z) \, dz=\frac{H^2-18 H-9 (H+1)^2 \log (10)+18 (H+1)^2 \log \left(\frac{3}{H}+3\right)-9}{10 (H-L)^2}\end{align}$
We replace $L=10^{d-1}, H=10^d-1$
$\displaystyle\begin{align} P_d&=(P_1+P_2)|_d= \frac{-2^{d+3} 5^{d+2}+100^d \left(180 \log \left(\frac{3}{10^d-1}+3\right)+9-9 \log (9)-80 \log (10)\right)+100}{\left(10-9\ 10^d\right)^2}\\ \lim_{d\to \infty }P_d&=\frac{1}{9}+\log (9)-\frac{80 \log (10)}{81} \approx 0.0341776 \end{align}$
Illustrations
I looked at $z$ being the fractional part of $\log_{10}(x)+\log_{10}(y),$ then the frequency distribution of $\lfloor 10^z\rfloor,$ results very close to exact count for $d=2:$
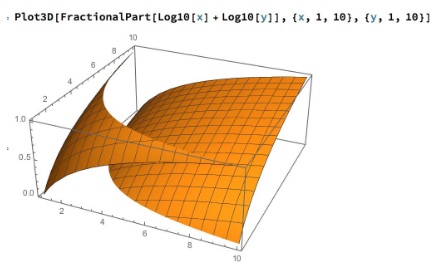
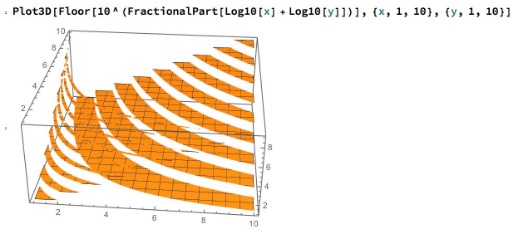
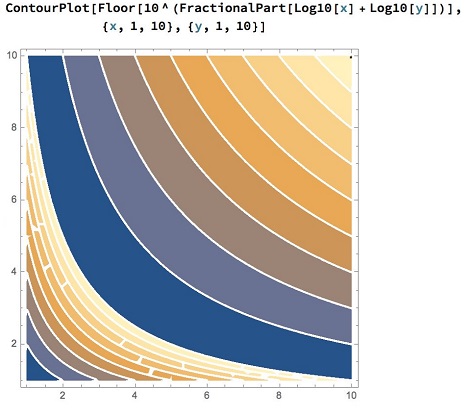
Acknowledgment
This is a modification of problem 165 from A Mathematical Orchard by M. I. Krusemeyer, G. T. Gilbert, L. C. Larson (MAA, 2012).
Solution 2 is by Amit Itagi; Solution 3 is by N. N. Taleb. Marcos Carreira has delivered the beautiful illustrations above.
|Contact| |Front page| |Contents| |Probability|
Copyright © 1996-2018 Alexander Bogomolny71534419