A Coin Tossing Surprise I

Problem

A Coin Tossing Surprise I, problem

Introduction

Since all four possible outcomes of two coin tosses are equiprobable, a couple of facts may seem surprising and, as such, have been discussed in a number of publications, e.g., by Martin Gardner in his The Colossal Book of Mathematics ( W. W. Norton & Company, 2005, p. 303).

First, as the transition diagram (Markov chain) below shows, except for an appearance at the first two tosses, $TT$ may only show up after $HT.$

Markov chain for one coin tossing, Markov chain

So perhaps the diagram makes it less surprising that the expected number of tosses to the first appearance of $HT$ is less than that for $TT.$ Below this phenomenon will acquire a more accurate estimate.

Solution to part 1

In the diagram below we only focus on achieving $HT:$

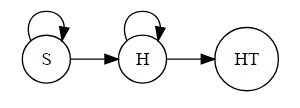
Markov chain for one coin tossing, Markov chain for HT

Assign a variable to each of the three nodes, say, $x,y,z$ that express the expected number of tosses in reaching our present destination, namely, $HT.$ Naturally, $z=0$ and was only added for the sake of uniformity. The three are combined into two equations:

$\displaystyle \begin{align} y &= 1 + \frac{1}{2}y +\frac{1}{2}z\\ x &= 1 + \frac{1}{2}x + \frac{1}{2}y. \end{align}$

The inclusion of $1$ in the equations is due to the fact that they describe the number of coin tosses and each tells us how these expectations are connected after one toss. The first equation yields $\displaystyle y=2,$ so that from the second $\displaystyle x=4.$

Solution to part 2

As in part 1, we introduce the variables $x,y,z,$ with $z=0,$ again:

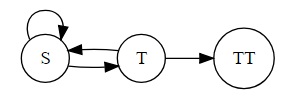
Markov chain for one coin tossing, Markov chain for TT

$\displaystyle \begin{align} y &= 1 + \frac{1}{2}x +\frac{1}{2}z\\ x &= 1 + \frac{1}{2}x + \frac{1}{2}y. \end{align}$

The second equation reduces to $\displaystyle x=y+\frac{1}{2}y,$ so that $\displaystyle y=\frac{2}{3}x.$ Then the first equation becomes $\displaystyle \frac{2}{3}x=1+\frac{1}{2}x,$ from which $x=6.$

Solution to part 3

Each of the four possible outcomes of two coin tosses is equiprobable and comes with the probability of $\displaystyle \frac{1}{4}.$ This is the only opportunity for $TT$ to come before $HT.$ It follows that $HT$ is three times more likely than $TT$ to show up first. In other words, the probability of $HT$ showing first is $\displaystyle\frac{3}{4}.$

71542398