Isoperimetric theorem and its variants

Problem

Let both ends of a string of length L be tied to a stick of length S. Among all plane regions enclosed by this contraption, find the one with the largest area.

Isoperimetric Theorem

Among all plane regions with a given perimeter a circle has the largest area.

For the sake of the current discussion I'll accept Isoperimetric Theorem as a known fact on which it's easy to base a solution to the original problem.

Remark

If S = 0 our problem degenerates into its extreme case - Isoperimetric Theorem.

Solution

In case S>0 let us try to reduce the problem to a known case. I'll cite from Polya's Induction and Analogy in Mathematics:

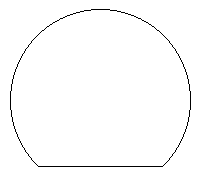
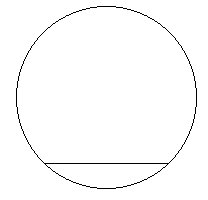
Lay down the stick. Its endpoints determine its position completely. Yet the string can take infinitely many shapes, forming an arbitrary curve with given length that connects the end points of the stick (see Figure 1.) One of the possible shapes of the string is a circular arc which includes a segment of a circle with the stick (Figure 2.) Complete the circle by adding another segment (Figure 3) and add the same segment to the shape formed by the stick and an arbitrary position of the string (Figure 4.) The circle in Figure 3 encloses the largest area among all curves with the same perimeter, and the one on Figure 4 is such a curve. Subtracting the same circular segment from the two figures, we find the result: the area surrounded by the stick and the string is maximum when the string forms a circular arc as in Figure 2.

Figure 1	Figure 2
Figure 3	Figure 4

Follow up

1. What if a string of a given length is attached to two rings sliding along a straight line? Describe position of the string that encloses the largest possible area.
2. Assume a string is attached to the end points of the graph y = sin(x) where -1 ≤ x ≤ 1. Same question.

(For a completely different theorem under the same name see An Isoperimetric Theorem.)

|Contact| |Front page| |Contents| |Generalizations| |Geometry| |Store|

Copyright © 1996-2012 Alexander Bogomolny