Polygon in a Rectangle

Every convex polygon of area 1 is contained in a rectangle of area 2.

Proof

The claim is certainly true for a triangle. Any triangle can be embedded in a rectangle of twice its area.

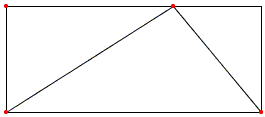
Interestingly, the more general fact follows from this simple observation. Let K be a convex polygon of area 1. Pick two most distant vertices of the polygon.

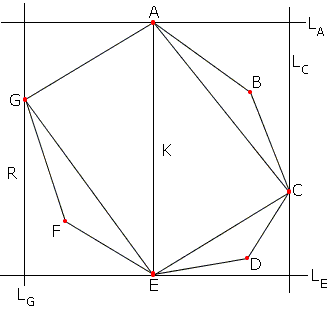
These are vertices A and E in the diagram. Through A and E draw lines L_A and L_E perpendicular to AE. Since the distance between A and E is the largest of all the distances between any two points of K, neither L_A or L_E meet K in points other than A and E. Draw a line perpendicular to L_A and L_E away from K on the right. Move towards K until it first touches K. The line will then share with K either a side of a vertex. In the diagram this is vertex C and the line is called L_C. Similarly, find a line perpendicular to L_A and L_E to the left from K and move it towards K until the first contact. This is line L_G in the diagram.

The four lines form a rectangle. Call it R. Line AE separates R into two smaller rectangles, say R_G and R_C.

Join A and E to C and G. The area of ΔAEG is half that of rectangle R_G. The area of ΔAEC is half that of rectangle R_C. The area of the quadrilateral ACEG is half that of R. Since K is convex, ACEG lies entirely within K and hence its area is at most 1. It follows that the area of R is at most 2. If need be, to answer the requirement it may be enlarged to enclose the area of 2.

References