Weitzenböck's Inequality

The applet below illustrates a geometric proof of Weitzenböck's Inequality.

For any triangle ABC with sides $a,$ $b,$ $c,$ and the area $S,$

$a^2 + b^2 + c^2 \ge 4\sqrt{3}S.$

This wonderful geometric proof is due to C. Alsina and R. B. Nelsen.

Explanation

References

C. Alsina and R. B. Nelsen, Geometric Proofs of Weitzenböck and Hadwiger-Finsler Inequalities, Mathematics Magazine, v. 81, No. 3, June 2008, pp. 216-219
C. Alsina, R. B. Nelsen, Charming Proofs, MAA, 2010, pp. 96-98

Theorem

For any $\Delta ABC$ with sides $a,$ $b,$ $c,$ and the area $S,$

(1)

$a^2 + b^2 + c^2 \ge 4\sqrt{3}S.$

Proof

Form, on the sides of $\Delta ABC,$ Napoleon triangles, $ABC',$ $BCA',$ $CAB'.$ For a triangle with all angles less than $120^{\circ},$ the three lines $AA',$ $BB',$ $CC'$ concur at Fermat's point of the triangle. The point solves the minimization problem: for all points $X,$ $XA + XB + XC$ attends its minimum at $F.$ If one of the angles is greater or equal to $120^{\circ}$ Fermat's point lies at the corresponding vertex.

Multiply (1) by $\sqrt{3}/4.$ The inequality becomes

(2)

$S_{a} + S_{b} + S_{c} \ge 3S,$

where S_{a} is the area of $\Delta BCA',$ etc.

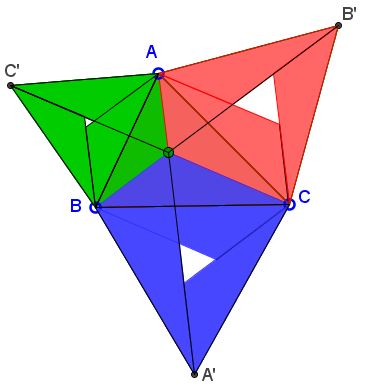
Witzenbrock's inequality, PWW

In fact, a stronger result holds. Let $F$ be interior to $\Delta ABC,$ with distances $x,$ $y,$ $z$ to $A,$ $B,$ $C,$ respectively. Let $S_{k}$ denote the area of an equilateral triangle with side $k.$ Then

(3)

$S_{a} + S_{b} + S_{c} = 3S + S_{|x - y|} + S_{|y - z|} + S_{|z - x|}.$

To see that (3) holds, observe that $F$ splits $\Delta ABC$ into three triangles each with angle $120^{\circ}$ at $F.$ This shows that the remaining angles in each triangle add up to $60^{\circ}.$ It follows that three copies of each of the triangles fit into the corresponding equilateral triangle leaving equilateral triangles with sides $|x - y|,$ $|y - z|,$ and $|z - x|.$

When F coincides with, say, vertex C, then

(4)

$S_{a} + S_{b} + S_{c} \ge S_{c} \ge 3S.$

Stronger than (1) is the Hadwiger-Finsler inequality: if $a,$ $b,$ $c$ are the sides of a triangle with area $S$ then

(5)

$a^2 + b^2 + c^2 \ge 4\sqrt{3}S + (a - b)^2 + (b - c)^2 + (c - a)^2.$

In terms of areas, the latter is equivalent to

(6)

$S_{a} + S_{b} + S_{c} \ge 3S + S_{|a - b|} + S_{|b - c|} + S_{|c - a|}.$

In case $F$ is internal to $\Delta ABC,$ this inequality is a consequence of (3) because

$|x - y| \ge |a - b|,$ etc.

To prove these, assume $a \ge b \ge c.$ Then by reflecting the triangle with sides $b,$ $x,$ $z$ in the segment $z$ leads to the following configuration:

Hadwiger-Finsler inequality

The triangle inequality (in the yellow triangle) then implies $y - x \ge a - b.$ The other two inequalities are established similarly. Thus from (3)

$\begin{align} S_{a} + S_{b} + S_{c} &= 3S + S_{|x - y|} + S_{|y - z|} + S_{|z - a|}\\ &\ge 3S + S_{|a - b|} + S_{|b - c|} + S_{|c - a|}. \end{align}$

In case where, say, angle $C$ is $120^{\circ}$ or more so that $F$ coincides with $C,$ $z = 0,$ $x = b$ and $y = a.$ The inequality in (4) is refined to

$S_{a} + S_{b} + S_{c} \ge 3S + S_{|a - b|} + S_{a} + S_{b}.$

Now observe that $a \ge |b - c|$ and $b \ge |c - a|$ from which, again, (6) follows.

Note that there is a generalization due to Dan Pedoe.

71548252