|
|
|
|
|
|
|
|
|
Reflections of a Point on the Circumcircle: What Is This About?
|
| Buy this applet What if applet does not run? |
Copyright © 1996-2008 Alexander Bogomolny
Reflections of a Point on the Circumcircle
The applet suggests the following theorem [Coxeter & Greitzer, p. 45, Honsberger, pp. 43-44]:
| The reflections of a point on the circumcenter of a triangle in the side lines of the latter are collinear with the orthocenter of the triangle. |
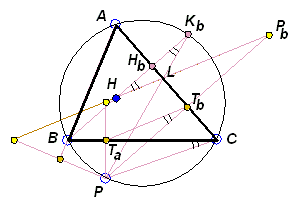
Let P be a point on the circumcenter of 
ABC. Ta
Note that the points Ta, Tb, Tc lie on the simson of P with respect to ABC. Also, the points Pa, Pb, Pc are the images of points Ta, Tb, Tc under the homothety with center P and coefficient 2. Thus we immediately see that the points Pa, Pb, Pc are collinear. It remains to be shown that the orthocenter H lies on the same straight line.
|
In the diagram, TaTb is the simson line ABC. To prove the assertion, we shall show that HPb||TaTb.
First, since PTa is perpendicular to BC and PTb is perpendicular to AC, the quadrilateral PTaTbC is cyclic. The inscribed angles TaTbP and TaCP stand on the same arc TaP and are, therefore equal:
| (1) |
 TaTbP = TaCP.
|
HPb is the reflection of KbP in AC, while HKb is perpendicular to AC. Therefore,
| (2) |
BKbP = KbHPb.
|
Angles BKbP and BCP (= TaCP) are equal as inscribed into the same circle and being subtended by the same arc BP:
| (3) |
BKbP = BCP.
|
The combination of (1)-(3) gives a crucial for the proof identity:
| (4) |
TaTbP = PbHHb.
|
Since one pair of the sides of these angles (PTb and HHb are both perpendicular to AC) are parallel, the same holds for the other pair of the sides: HPb||TaTb.
Corollary
The simson line of a point P on the circumcircle of a triangle bisects the segment PH joining the point to the orthocenter H.
References
- H.S.M. Coxeter, S.L. Greitzer, Geometry Revisited, MAA, 1967
- R. Honsberger, Episodes in Nineteenth and Twentieth Century Euclidean Geometry, MAA, 1995.
Copyright © 1996-2008 Alexander Bogomolny
| 29284647 |  |
|