A Line in Triangle Through the Circumcenter

The applet below illustrates the following statement I came across at the WOOT of the site:

Let O be the circumcenter of ΔABC. A line through O intersects the sides AB and AC at M and N, respectively. Let S and R be the midpoints of BN and CM. respectively. Prove that ∠ROS = ∠BAC.

---

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at http://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

---

Solution

|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|

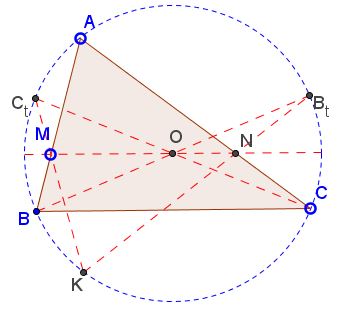
The problem is easily solved with a variant of Pascal's Hexagram Theorem. This is how.

Let BB_t and CC_t be two diameters of the circumcircle. First, observe that a homothety with center B and coefficient 2 maps O to B_t and R to N. It follows that OR||NB_t. Similarly, OS||MC_t. Let B_t and MC_t meet at K. The proof is based on the fact that K lies on the circle. This may not be immediately obvious and I deal with this assertion on a separate page.

The inscribed angles at B_t and C_t add up to the inscribed angle at A, i.e. ∠BAC, implying

∠BOR + ∠COS = ∠BAC.

On the other hand, since ∠BOC is the central angle subtended by the same arc as the inscribed ∠BAC, we have

∠BOC = 2∠BAC.

Finally,

The fact that K lies on the circle is a special reformulation of Pascal's theorem.

Chasing Inscribed Angles

• Munching on Inscribed Angles
• More On Inscribed Angles
• Inscribed Angles
• Tangent and Secant
• Angles Inscribed in an Absent Circle
• A Line in Triangle Through the Circumcenter
• Angle Bisector in Parallelogram
• Phantom Circle and Recaptured Symmetry
• Cherchez le quadrilatere cyclique
• Cyclic Quadrilateral, Concurrent Circles and Collinear Points
• Parallel Lines in a Cyclic Quadrilateral

|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|