Three Orthogonal Circles Through Three Given Points

This is Problem 1 from the III Moscow State University Olympiad (1937), final competition.

Given three noncollinear points, construct three pairwise orthogonal circles each passing through a pair of the points.

To remind, the angle between two curves is defined as the angle between their tangents at the point of intersection. When the curves are circles, the radii to the common point (which are perpendicular to the tangents) form the same angle. This remark suggests a reformulation:

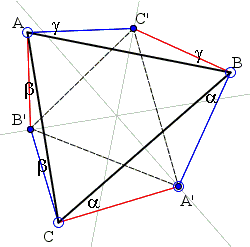
Given three noncollinear points A, B, C, find three points A', B', C' such that A'B = A'C, B'A = B'C, C'A = C'B and also A'B ⊥ C'B, A'C ⊥ B'C, B'A ⊥ C'A.

An analysis of the configuration leads to a simple solution and also shows that the problem can be readily generalized.

One generalization concerns the angles A'BC', C'AB', etc. For the problem to be solvable these angles need not be 90° or be equal, for that matter. In the applet below, to keep the interface simple, the angles are all equal and the scroll bar lets one modify their common magnitude.

Another generalization concerns the lines where points A', B', C' are sought. In the original problem these points lie on the perpendicular bisectors of ΔABC. The problem is solvable for a pretty general configuration of three lines:

Given three noncollinear points A, B, C and three lines L_A, L_B, L_C, find three points A' ∈ L_A, B'∈ L_B, C' ∈ L_C, such that the angles A'BC', C'AB' and B'CA' are equal to the given angle ω.

The applet below illustrates the latter problem with several choices of the three lines. In all cases, the three lines are concurrent and the configuration seems to possess an additional property.

Choose point A' on L_A. Rotate line BA' through angle ω around B and let C' be the intersection of its image with LC. Next rotate AC' around A and let B' be the intersection of its image with L_B. On the third leg, rotate CB' around C and let its intersection with L_A be A''. From A'' obtain B'', C'', A''' in the manner just described. For all choices of the lines below and the angle ω, A''' = A'. The three steps define a function f: L_A → L_A. What the applet shows is that, for certain selections of the lines, f is an involution which means that, repeated twice, the function leaves all the points unmoved: f(f(x)) = x. In other words, the involution is a function that coincides with its inverse: f = f^-1.

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at https://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

What if applet does not run?

As a last touch, observe that whenever lines L pass through the vertices A, B, C, the triangles ABC and A'B'C' are naturally perspective, with the point of concurrency of the lines as the center of perspective. The center of perspective is independent of angle ω.

For the original case, where the lines are the perpendicular bisectors of the sides of ΔABC and do not pass through the vertices, triangles ABC and A'B'C' are still perspective, with the center of perspective being a function of ω.

Given three noncollinear points A, B, C, find three points A', B', C' such that A'B = A'C, B'A = B'C, C'A = C'B and also A'B ⊥ C'B, A'C ⊥ B'C, B'A ⊥ C'A.

For simplicity, I shall denote the vertex angles of ΔABC by the same latter as vertices: A, B, C. On the other hand, A', B', C' will denote the angles CA'B, AB'C, BC'A. Triangles CA'B, AB'C, BC'A are isosceles with the base angles, &alpha, β and γ. The latter angles will be thought negative if the corresponding vertex falls inside ΔABC. Besides having A + B + C = 180°, the problem stipulates that

	β + A + γ	= 90°
	γ + B + α	= 90°
	α + C + β	= 90°

Adding the three together gives α + β + γ = 45°. Substituting this into the first action, we get A = α + 45°. This gives an expression for

	A'	= 180° - 2α
		= 180° - 2(A - 45°)
		= 270° - 2A.

This means that A' lies on the arc of a circle through B and C with angular measure 360° - (270° - 2A) = 90° + 2A. A' is therefore the intersection of that arc with the perpendicular bisector of BC. Points (and angles) B' and C' are treated similarly. There are, in principle, 2 solutions.

72392729