The Plain Butterfly Theorem
The Butterfly theorem is an engaging statement in elementary geometry that may be looked at from several perspectives and that admits several non-trivial generalizations.
The Butterfly Theorem
Let M be the midpoint of a chord PQ of a circle, through which two other chords AB and CD are drawn; AD cuts PQ at X and BC cuts PQ at Y. Prove that M is also the midpoint of XY.
A careful analysis of several available proofs reveals a few (e.g., proofs 2, 14, 16, 18) that do not at all relate to a chord PQ. These proofs depend only on the fact that the given point M lies on a given line PQ perpendicular to the diameter of the circle through M. This allows for a reformulation of the theorem.
The Plain (Chordless) Butterfly Theorem
Given a quadrilateral ACBD inscribed in a circle C(O), let M be the intersection of the diagonals AB and CD and L a line through M perpendicular to the OM. Assume that side AD of the quadrilateral ACBD meets L in X, and side BC meets L in Y. Then
The applet below illustrates the latter formulation.
The new formulation has a definite advantage over the standard one. Firts of all, it shows that the theorem holds even when M lies outside the circle and, therefore, does not serve a midpoint of any chord:

Also, the commonly used illustration of the Butterfly theorem places points A and C on one side of line L, and points B and D on the other:
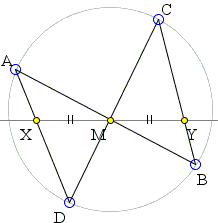
This is of course only one of two possibilities as illustrated below:

The latter case makes it quite obvious that, in general, on the line perpendicular to OM there are two pairs of points equidistant from M. These are the points of intersections with that line of the pairs of opposite sides of the given quadrilateral. There are, of course, two such pairs, as there are two pairs of butterfly wings: one of these is crossed by line L, the other is not.
As I mentioned above, several of the known proofs, never relate to the existence of points P and Q, that is, to the fact that PQ is indeed a chord in the given circle. It is an amusing exercise to attempt to adapt the other proofs that explicitly address points P and Q in some manner.
As a matter of fact, the following two theorems have been published in 2002.
Theorem 1
Let the quadrangle ACBD be inscribed into the circle C(O) with center O. Let the line S connect the center O with one of the three diagonal points of the quadrangle, say M. Then the line L through M perpendicular to
Theorem 2
Let the quadrangle ACBD be inscribed into the circle C(O) with center O. On any given line L let T denote the pedal point of O. If T is the midpoint of the two points
The given points A, B, C, D should be regarded as the basic points of a pencil of conics which contains the circle C(O). In such case the pairs of opposite sides of the given quadrangle are three degenerated conics of the pencil. Due to the Sturm-Desargues theorem the conics of this pencil intersect any line (not passing through A, B, C, D) in pairs of points of an involution. The butterfly point is one of the two fixed points; the other is a point at infinity. There are two conics of the pencil tangent to L. One touches at the butterfly point, the other is always a hyperbola.
Note that in Theorem 1 the butterfly point is one of the diagonal points of the quadrangle inscribed into the circle C(O). So, only three choices are possible. On the other hand, Theorem 2 says nothing about the existence or uniqueness of the so-called butterfly point M and about its constructive determination.
References
- A. Sliepcevic, A New Generalization of the Butterfly Theorem, Journal for Geometry and Graphics, Volume 6 (2002), No. 1, 61-68.
Butterfly Theorem and Variants
- Butterfly theorem
- 2N-Wing Butterfly Theorem
- Better Butterfly Theorem
- Butterflies in Ellipse
- Butterflies in Hyperbola
- Butterflies in Quadrilaterals and Elsewhere
- Pinning Butterfly on Radical Axes
- Shearing Butterflies in Quadrilaterals
- The Plain Butterfly Theorem
- Two Butterflies Theorem
- Two Butterflies Theorem II
- Two Butterflies Theorem III
- Algebraic proof of the theorem of butterflies in quadrilaterals
- William Wallace's Proof of the Butterfly Theorem
- Butterfly theorem, a Projective Proof
- Areal Butterflies
- Butterflies in Similar Co-axial Conics
- Butterfly Trigonometry
- Butterfly in Kite
- Butterfly with Menelaus
- William Wallace's 1803 Statement of the Butterfly Theorem
- Butterfly in Inscriptible Quadrilateral
- Camouflaged Butterfly
- General Butterfly in Pictures
- Butterfly via Ceva
- Butterfly via the Scale Factor of the Wings
- Butterfly by Midline
- Stathis Koutras' Butterfly
- The Lepidoptera of the Circles
- The Lepidoptera of the Quadrilateral
- The Lepidoptera of the Quadrilateral II
- The Lepidoptera of the Triangle
- Two Butterflies Theorem as a Porism of Cyclic Quadrilaterals
- Two Butterfly Theorems by Sidney Kung
- Butterfly in Complex Numbers
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny71547484
