Lean Napoleon's Triangles: What is this about?
A Mathematical Droodle

Explanation

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

The applet attempts to suggest the following statement [Garfunkel, Stahl]:

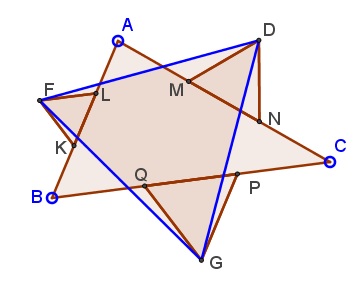
Proof

The proof is said to be computational but not tedious.

ΔAKF is isosceles, with ∠AKF = 120°. So its base angles (KAF and AFK) are both 30°. It follows that ∠AFL = 90° which makes ΔAFL right. If, as usual, AB = c, then in ΔAFL, AL = 2c/3 and LF = c/3. By the Pythagorean theorem, (AF)² = c²/3.

Similarly, ΔAMD is right and (AD)² = b²/3.

We are now in a position to apply the Law of Cosines in ΔADF to determine the length of DF. Note that ∠DAF = ∠A + 60°.

(DF)² = b²/3 + c²/3 - 2bc/3·cos(A + 60°)   = b²/3 + c²/3 - 2bc/3·cos(A)cos(60°) + 2bc/3·sin(A)sin(60°)   = b²/3 + c²/3 - 2bc·cos(A)/6 + 2bc/3·sin(A)√3/2   = b²/3 + c²/3 - (b² + c² - a²)/6 + 2√3/3·S   = (a² + b² + c²)/6 + 2√3/3·S,

where S is the area of ΔABC. (We again used Law of Cosines and also a formula for the area of a triangle.) The expression is symmetric in a, b, c so that (GD)² and (GF)² are bound to be equal to the same quantity, proving that indeed ΔGDF is equilateral.

Observe that the above derivation only works when triangles KLF, MND, and PQG are drawn outwardly on the sides of ΔABC. If they are drawn inwardly, then ∠DAF may equal either ∠A - 60° or 60° - ∠A. In both cases we would obtain

(DF)² = (a² + b² + c²)/6 - 2√3/3·S,

with the same conclusion. Thus we are led to two equilateral triangles related to a base ΔABC. From the above relations it follows that the difference in areas of the two triangles is exactly that of ΔABC.

As James Bond drops on an occasion in "Tomorrow Never Dies", "They'll publish anything these days."

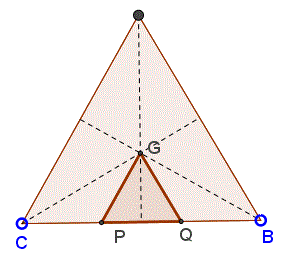
As a matter of fact, the triangle GDF is exactly Napoleon's triangle, because points G, D, F are the centers of the equilateral triangle formed on the sides of ΔABC:

References

1. J. Garfunkel, S. Stahl, The Triangle Reinvestigated, Am Math Monthly, Vol. 72, No. 1. (Jan., 1965), pp. 12-20

Napoleon's Theorem

• Napoleon's Theorem
• A proof with complex numbers
• A second proof with complex numbers
• A third proof with complex numbers
• Napoleon's Theorem, Two Simple Proofs
• Napoleon's Theorem via Inscribed Angles
• A Generalization
• Douglas' Generalization
• Napoleon's Propeller
• Napoleon's Theorem by Plane Tessellation
• Fermat's point
• Kiepert's theorem
• Lean Napoleon's Triangles
• Napoleon's Theorem by Transformation
• Napoleon's Theorem via Two Rotations
• Napoleon on Hinges
• Napoleon on Hinges in GeoGebra
• Napoleon's Relatives
• Napoleon-Barlotti Theorem
• Some Properties of Napoleon's Configuration
• Fermat Points and Concurrent Euler Lines I
• Fermat Points and Concurrent Euler Lines II
• Escher's Theorem
• Circle Chains on Napoleon Triangles
• Napoleon's Theorem by Vectors and Trigonometry
• An Extra Triple of Equilateral Triangles for Napoleon
• Joined Common Chords of Napoleon's Circumcircles
• Napoleon's Hexagon
• Fermat's Hexagon
• Lighthouse at Fermat Points
• Midpoint Reciprocity in Napoleon's Configuration
• Another Equilateral Triangle in Napoleon's Configuration
• Yet Another Analytic Proof of Napoleon's Theorem
• Leo Giugiuc's Proof of Napoleon's Theorem
• Gregoie Nicollier's Proof of Napoleon's Theorem
• Fermat Point Several Times Over

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny