Circles in Morley's Triangles: What is this about?
A Mathematical Droodle

(The numbers are clickable and so may be modified.)

Explanation. See also the page on Morley Constellation.

Copyright © 1996-2009 Alexander Bogomolny

What's happening is this. Let r be a number between 0 and 1. We shall perform a construction similar to but more general than Morley's. For vertex A, measure angles rA from both sides, and similarly for the vertices B and C. The lines adjacent to one of the sides of the given triangle intersect forming seven triangles: the middle one -- Morley's if r = 1/3 -- and 3 pairs of "opposite" triangles. It appears that the lines joining incenters of the opposite triangles are concurrent. It also seems to be true of the circumcenters. We can prove the latter when r = 1/3.

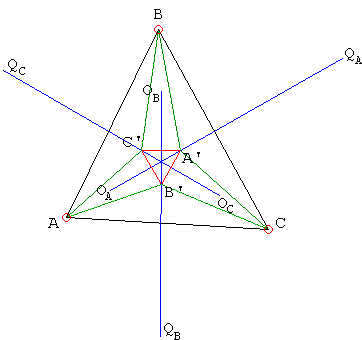
Theorem (by Nikos Dergiades with an important correction by Samuele Mongodi)

Let A'B'C' denote the Morley triangle. Denote the circumcenters of triangles AB'C', BC'A', and CA'B' O_A, O_B and O_C, and those of triangles BCA', CAB', and ABC' Q_A, Q_B and Q_C, respectively. Let angles A = 3x, B = 3y, C = 3z.

Since it's known that BA'C' = 60^o + z, BQ_AA' = 2z (as central angle subtending the same arc as the inscribed angle BCA') and Q_AA'B = 90^o - z (see below) we have Q_AA'C' = 150^o, which means that the line Q_AA' is the bisector of angle A' in Morley's triangle A'B'C'. Hence, it's also the perpendicular bisector of B'C'. As such, it passes through O_A.

Similar statements are true with regard to O_BQ_B and O_CQ_C, which means that the three lines meet at the center of Morley's triangle.

(Some of the triangles have already been considered elsewhere.)

Samuele Mongodi found a flaw in the original Nikos' argument and offered the following fix:

Since Q_A is the circumcenter of BCA',BA'Q_A is isosceles, so that Q_ABA' = Q_AA'B. In combination with BQ_AA' = 2z, as noted by Nikos, this yields

QAA'B = (1800 - 2z)/2 = 900 - z,

as claimed.

Copyright © 1996-2009 Alexander Bogomolny